
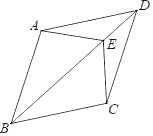
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果∠BDC=30°,DE=2,EC=3,求CD的长.
【答案】(1)证明见解析;(2)CD的长为2![]() .
.
【解析】
(1)首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,易得∠CDB=∠CBD,可得BC=CD,易得AD=BC,利用平行线的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形;
(2)作EF⊥CD于F,在Rt△DEF中,根据30°的性质和勾股定理可求出EF和DF的长,在Rt△CEF中,根据勾股定理可求出CF的长,从而可求CD的长.
证明:(1)在△ADE与△CDE中,
 ,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
(2)作EF⊥CD于F.
∵∠BDC=30°,DE=2,
∴EF=1,DF=![]() ,
,
∵CE=3,
∴CF=2![]() ,
,
∴CD=2![]() +
+![]() .
.
 .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中网格上按要求画出图形,并回答问题:
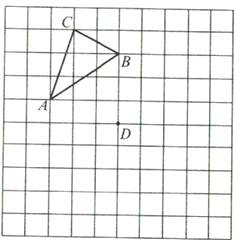
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() ______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“◇”和“☆”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植.
(1)观察图形,寻找规律,并填写下表:


(2)求出第![]() 个图形中甲种植物和乙种植物的株数;
个图形中甲种植物和乙种植物的株数;
(3)是否存在一种种植方案,使得乙种植物的株数是甲种植物的株数的2倍?若存在,请你写出是第几个方案,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
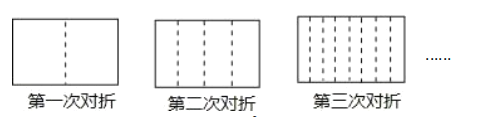
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到![]() 条折痕,那么对折四次可以得到( )条折痕.如果对折
条折痕,那么对折四次可以得到( )条折痕.如果对折![]() 次, 可以得到( )条折痕
次, 可以得到( )条折痕
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com