[题目]如图在中...则( )A. 1:8:27 B. 1:4:9 C. 1:8:36 D. 1:9:36 题目和参考答案——青夏教育精英家教网—

【题目】如图在中，，，则（）

A. 1:8:27 B. 1:4:9 C. 1:8:36 D. 1:9:36

【答案】A

【解析】

根据DE//FG//BC,可判定△ADE∽△AFG∽△ABC,
根据AD:DF:FB=1:2:3,可得AD:AF:AB=AD:(AD+DF):(AD+DF+FB)=1:(1+2):(1+2+3)=1:3:6,
再根据相似三角形的面积比等于相似比的平方倍可得:S△ADE：S△AFG：S△ABC=1:9:36,继而得到:
S△ADE：S DFGE：S FBCG=1：(9-1)：(36-9)=1：8：27,

因为DE//FG//BC,所以△ADE∽△AFG∽△ABC,
因为AD:DF:FB=1:2:3,

所以AD:AF:AB=AD:(AD+DF):(AD+DF+FB)=1:(1+2):(1+2+3)=1:3:6,
S△ADE：S△AFG：S△ABC=1:9:36,
S△ADE：S DFGE：S FBCG=1：(9-1)：(36-9)=1：8：27,

故选A.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

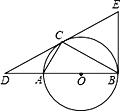
【题目】已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA∶AB=1∶2．

（1）求∠CDB的度数；

（2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】用“※”定义一种新运算：对于任意有理数a和b，规定a※b＝ab2+2ab+a．

如：1※2＝1×22+2×1×2+1＝9

（1）（﹣2）※3＝　；

（2）若※3＝16，求a的值；

（3）若2※x＝m，（x）※3＝n（其中x为有理数），试比较m，n的大小．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】用“◇”和“☆”分别代表甲种植物和乙种植物，为了美化环境，采用如图所示的方案种植．

（1）观察图形，寻找规律，并填写下表：

（2）求出第个图形中甲种植物和乙种植物的株数；

（3）是否存在一种种植方案，使得乙种植物的株数是甲种植物的株数的2倍？若存在，请你写出是第几个方案，若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，一次函数的图象与轴交于点，与正比例函数的图象相交于点，且.

（1）分别求出这两个函数的解析式；

（2）求的面积；

（3）点在轴上，且是等腰三角形，请直接写出点的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知在中，，点D沿BC自B向C运动点D与点B、C不重合，作于E，于F，则的值　　

A. 不变 B. 增大 C. 减小 D. 先变大再变小

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.

【答案】 .

【解析】试题分析：

根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.

试题解析：

列表如下：

	1	2	3	4
1	（1，1）	（1，2）	（1，3）	（1，4）
2	（2，1）	（2，2）	（2，3）	（2，4）
3	（3，1）	（3，2）	（3，3）	（3，4）
4	（4，1）	（4，2）	（4，3）	（4，4）