
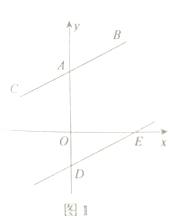
【题目】已知,点![]() ,点
,点![]() 分别在
分别在![]() 轴正半轴和负半轴上,
轴正半轴和负半轴上,![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在![]() 和
和![]() 内作射线
内作射线![]() ,
,![]() ,分别与过
,分别与过![]() 点的直线交于第一象限内的点
点的直线交于第一象限内的点![]() 和第三象限内的点
和第三象限内的点![]() .
.
①如图2,若![]() ,
,![]() 恰好分别平分
恰好分别平分![]() 和
和![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,当
,当![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.

【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用二次根式的性质求得![]() 的值,根据三角形内角和定理结合已知条件构建方程,再利用平行线的性质即可求解;
的值,根据三角形内角和定理结合已知条件构建方程,再利用平行线的性质即可求解;
(2)①过M作MF∥AB,NG∥AB,根据角平分线的性质和平行线的性质,求得∠AMN-∠ENM =![]() –
–![]() ,再根据平行线的性质和三角形内角和定理即可求解;
,再根据平行线的性质和三角形内角和定理即可求解;
②设![]() ,
,![]() ,则
,则![]() ,
,![]() ,根据①的解法即可求得∠AMN-∠ENM=
,根据①的解法即可求得∠AMN-∠ENM=![]() ,再解不等式组即可求解.
,再解不等式组即可求解.
(1)∵![]() ,整理得:
,整理得:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴∠BAD=4∠OED,
∵∠OED+∠ODE=90![]() ①,∠BAD+∠ODE=180
①,∠BAD+∠ODE=180![]() ,即4∠OED +∠ODE=180
,即4∠OED +∠ODE=180![]() ②,
②,
联立①②解得:∠OED=30![]() ,∠ODE=60
,∠ODE=60![]() ,
,
∵AB∥DE,
∴∠CAD=∠ODE=60![]() ;
;
(2)①∵AM、EN是∠BAO、∠DEO的平分线,
∴设![]() ,
,![]() ,
,
过M作MF∥AB,NG∥AB分别交AD于F,G,
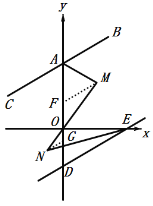
∵AB∥DE,
∴AB∥MF∥NG∥DE,
∴∠FMA=∠BAM=![]() ,∠FMN=∠MNG,∠GNE=∠NED=
,∠FMN=∠MNG,∠GNE=∠NED=![]() ,
,
∴∠AMN=∠FMA+∠FMN=![]() +∠FMN,
+∠FMN,
∠ENM=∠GNE +∠MNG =![]() +∠FMN,
+∠FMN,
∴∠AMN-∠ENM=![]() +∠FMN-
+∠FMN-![]() -∠FMN=
-∠FMN=![]() –
–![]() ;
;
∵∠ODE+∠OED=∠ODE+2![]() =90
=90![]() ,
,
∵AB∥DE,
∴∠BAD+∠ODE=180![]() ,即
,即![]() +∠ODE=180
+∠ODE=180![]() ,
,
∴![]() –
–![]() =90
=90![]() ,
,
∴∠AMN-∠ENM=![]() –
–![]() =45
=45![]() ;
;
②∵![]() ,
,![]() ,
,
∴设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
过M作MF∥AB,NG∥AB分别交AD于F,G,
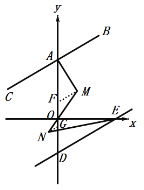
∵AB∥DE,
∴AB∥MF∥NG∥DE,
∴∠FMA=∠BAM=![]() ,∠FMN=∠MNG,∠GNE=∠NED=
,∠FMN=∠MNG,∠GNE=∠NED=![]() ,
,
∴∠AMN=∠FMA+∠FMN=![]() +∠FMN,
+∠FMN,
∠ENM=∠GNE +∠MNG =![]() +∠FMN,
+∠FMN,
∴∠AMN-∠ENM=![]() +∠FMN-
+∠FMN-![]() -∠FMN=
-∠FMN=![]() –
–![]() =
=![]() ;
;
∵∠ODE+∠OED=∠ODE+![]() =90
=90![]() ,
,
∵AB∥DE,
∴∠BAD+∠ODE=180![]() ,即
,即![]() +∠ODE=180
+∠ODE=180![]() ,
,
∴![]() –
–![]() =90
=90![]() ,即
,即![]() –
–![]() =
=![]() ,
,
∴∠AMN-∠ENM=![]() =
=![]() ;
;
∵![]() ,
,
∴![]() ,
,
解不等式![]() ,化简得:
,化简得:![]() ,
,
解得:![]() ,
,
解不等式![]() ,化简得:
,化简得:![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.

(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党中央“下好一盘棋,共护一江水”的号召,某治污公司决定购买甲、乙两种型号的污水处理设备共10台.经调查发现:购买一台甲型设备比购买一台乙型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元,且一台甲型设备每月可处理污水240吨,一台乙型设备每月可处理污水200吨.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)若治污公司购买污水处理设备的资金不超过109万元,月处理污水量不低于2080吨.
①求该治污公司有几种购买方案;
②如果为了节约资金,请为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
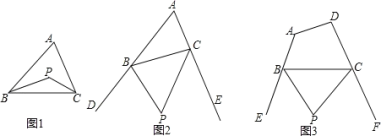
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于点A,交x轴于B,C两点(点B在点C的左侧),已知C点坐标为(6,0).
(1)求此抛物线的解析式;
(2)连结AB,过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与抛物线的对称轴l相切,先补全图形,再判断直线BD与⊙C的位置关系并加以证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间.问:当点P运动到什么位置时,△PAC的面积最大?求出△PAC的最大面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
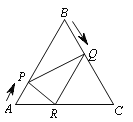
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com