【题目】如图所示，在△ABC中，AD是∠BAC的平分线，AH是BC边上的高，H是垂足．如果∠B=65°，∠C=45°，求∠DAH的度数．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点P从A点出发沿A→C→B路径向终点运动，终点为B点；点Q从B点出发沿B→C→A路径向终点运动，终点为A点．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，当一个点到达终点时另一个点也停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．设运动时间为t秒，则当t=______秒时，△PEC与△QFC全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图．在数学活动课中，小明剪了一张△ABC的纸片，其中∠A=60°，他将△ABC折叠压平使点A落在点B处，折痕DE，D在AB上，E在AC上．
（1）请作出折痕DE；（要求：尺规作图，不写作法，保留作图痕迹）
（2）判断△ABE的形状并说明；
（3）若AE=5，△BCE的周长为12，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
（1）如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
（2）若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，四边形ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件：
；
；
是BC的中点；
：
：3，其中能推出
∽
的有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC是等边三角形，P为平面内的一个动点，BP=BA，0<∠PBC<180 ，DB平分∠PBC，且DB=DA．
（1）当BP与BA重合时（如图1），求∠BPD的度数；
（2）当BP在∠ABC的内部时(如图2)，求∠BPD的度数；
（3）当BP在∠ABC的外部时，请你直接写出∠BPD的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标
， 纵坐标
的对应值如下表：
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法正确的是 ．
①抛物线与轴的一个交点为
； ②抛物线与轴的交点为
；
③抛物线的对称轴是：直线
； ④在对称轴左侧随增大而增大.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：
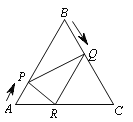
（1）当t＝2时，判断△BPQ的形状，并说明理由；
（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；
（3）作QR//BA交AC于点R，连结PR，当t为何值时，△APR∽△PRQ？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
