
【题目】如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:![]() ;
;![]() ;
;![]() 是BC的中点;
是BC的中点;![]() :
:![]() :3,其中能推出
:3,其中能推出![]() ∽
∽![]() 的有
的有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
根据四边形ABCD为正方形,可得AB=BC=CD,∠B=∠C=90°,由于E为CD中点,所以CD=2CE,即AB=BC=2CE, ①当∠APB=∠EPC时,结合∠B=∠C,利用两角分别对应相等的两三角形相似,可判定△ABP∽△ECP, ②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP, ③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP,④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,根据两边对应成比例且夹角相等的两个三角形相似,可判定△ABP∽△ECP相似
∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP,
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP,
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP,
④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,
可推出△ABP∽△ECP相似,故选B.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.

(1)求单摆的长度;
(2)求从点A摆动到点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
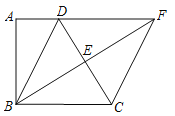
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=3cm,∠B=30°,点D在BC边上由C向B匀速运动(D不与B、C重合),匀速运动速度为1cm/s,连接AD,作∠ADE=30°,DE交线段AC于点E.
(1)在此运动过程中,∠BDA逐渐变 (填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD= .
(2)点D运动3s后到达图2位置,则CD= .此时△ABD和△DCE是否全等,请说明理由;
(3)在点D运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度(请直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮同学为了巩固自己对平行四边形判定知识的掌握情况,设计了一个游戏,他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上,卡片如图,他将卡片正面朝下反扣在桌面上,洗匀后从中随机抽取两张,然后根据卡片上的两个条件判断四边形ABCD是否为平行四边形,请你用列举法(列表法或树状图法)求出他能够判定四边形ABCD为平行四边形的概率.(卡片可用a、b、c、d表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:在△ABC中,∠B=∠C,点D在BC边上(点B、C除外),点E在AC边上,且∠ADE=∠AED,连接DE.
(1)如图①,若∠B=∠C=45,
①当∠BAD=60时,求∠CDE的度数;
②试猜想∠BAD与∠CDE的数量关系,并说明理由.
(2)深入探究:如图②,若∠B=∠C,但∠C≠45,其他条件不变,试探究∠BAD与∠CDE的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com