
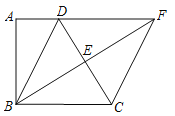
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:“39”.邻座的乘客十分惊奇,忙间其中计算的奥妙.
你知道怎样迅速准确的计算出结果吗?请你按下面的步骤试一试:
第一步:∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴能确定59319的立方根是个两位数.
第二步:∵59319的个位数是9,![]()
∴能确定59319的立方根的个位数是9.
第三步:如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3,因此59319的立方根是39.
(解答问题)
根据上面材料,解答下面的问题
(1)求110592的立方根,写出步骤.
(2)填空:![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )

A. 甲正确,乙不正确B. 甲不正确,乙正确
C. 甲、乙都正确D. 甲、乙都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
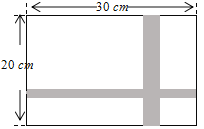
【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在数学活动课中,小明剪了一张△ABC的纸片,其中∠A=60°,他将△ABC折叠压平使点A落在点B处,折痕DE,D在AB上,E在AC上.
(1)请作出折痕DE;(要求:尺规作图,不写作法,保留作图痕迹)
(2)判断△ABE的形状并说明;
(3)若AE=5,△BCE的周长为12,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:![]() ;
;![]() ;
;![]() 是BC的中点;
是BC的中点;![]() :
:![]() :3,其中能推出
:3,其中能推出![]() ∽
∽![]() 的有
的有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
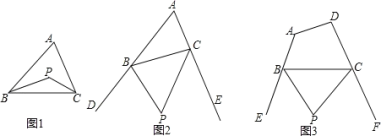
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com