
ЎѕМвДїЎїОТ№ъЦР¶«ІїµШЗшОнцІМмЖшЗчУЪСПЦШЈ¬»·ѕіЦОАнТСїМІ»ИЭ»єЈ®ОТКРДіµзЖчЙМіЎёщѕЭГсЦЪЅЎїµРиТЄЈ¬ґъАнПъКЫДіЦЦјТУГїХЖшѕ»»ЇЖчЈ¬ЖдЅшјЫКЗ200ФЄ/МЁЈ®ѕ№эКРіЎПъКЫєу·ўПЦЈєФЪТ»ёцФВДЪЈ¬µ±КЫјЫКЗ400ФЄ/МЁК±Ј¬їЙКЫіц200МЁЈ¬ЗТКЫјЫГїЅµµН10ФЄЈ¬ѕНїЙ¶аКЫіц50МЁЈ®Иф№©»хЙМ№ж¶ЁХвЦЦїХЖшѕ»»ЇЖчКЫјЫІ»ДЬµНУЪ300ФЄ/МЁЈ¬ґъАнПъКЫЙМГїФВТЄНкіЙІ»µНУЪ450МЁµДПъКЫИООсЈ®
ЈЁ1Ј©КФИ·¶ЁФВПъКЫБїyЈЁМЁЈ©УлКЫјЫxЈЁФЄ/МЁЈ©Ц®јдµДєЇКэ№ШПµКЅЈ»ІўЗуіцЧФ±дБїxµДИЎЦµ·¶О§Ј»
ЈЁ2Ј©µ±КЫјЫxЈЁФЄ/МЁЈ©¶ЁОЄ¶аЙЩК±Ј¬ЙМіЎГїФВПъКЫХвЦЦїХЖшѕ»»ЇЖчЛщ»сµГµДАыИуwЈЁФЄЈ©ЧоґуЈїЧоґуАыИуКЗ¶аЙЩЈї
Ўѕґр°ёЎїЈЁ1Ј©y=©Ѓ5x+2200ЈЁ300ЎЬxЎЬ350Ј©Ј»ЈЁ2Ј©КЫјЫ¶ЁОЄ320ФЄ/МЁК±Ј¬ЙМіЎГїФВПъКЫХвЦЦїХЖшѕ»»ЇЖчЛщ»сµГµДАыИуwЧоґуЈ¬ЧоґуАыИуКЗ72000ФЄ
ЎѕЅвОцЎїКФМв·ЦОцЈє(1)ЎўПъКЫБї=200+50ЎБ(ЅµјЫµДКэБїЎВ10)µГіцґр°ёЈ»(2)ЎўёщѕЭ№©»хЙМ№ж¶ЁХвЦЦїХЖшѕ»»ЇЖчКЫјЫІ»ДЬµНУЪ300ФЄ/МЁЈ¬ґъАнПъКЫЙМГїФВТЄНкіЙІ»µНУЪ450МЁЈ¬µГіцІ»µИКЅЧйЈ¬ґУ¶шµГіцxµДИЎЦµ·¶О§Ј»(3)ЎўёщѕЭЧЬАыИу=µҐјюАыИуЎБКэБїµГіцєЇКэ№ШПµКЅЈ¬И»єуёщѕЭ¶юґОєЇКэµДРФЦКµГіцЧоґуЦµ.
КФМвЅвОцЈє(1)ЎўёщѕЭМвЦРМхјюПъКЫјЫГїЅµµН10ФЄЈ¬ФВПъКЫБїѕНїЙ¶аКЫіц50МЁЈ¬
ФтФВПъКЫБїyЈЁМЁЈ©УлКЫјЫxЈЁФЄ/МЁЈ©Ц®јдµДєЇКэ№ШПµКЅЈєy=200+50ЎБ![]() Ј¬
Ј¬
»ЇјтµГЈєy=-5x+2200Ј»
(2)ЎўёщѕЭ№©»хЙМ№ж¶ЁХвЦЦїХЖшѕ»»ЇЖчКЫјЫІ»ДЬµНУЪ300ФЄ/МЁЈ¬ґъАнПъКЫЙМГїФВТЄНкіЙІ»µНУЪ450МЁЈ¬ ФтxЎЭ300ЗТ5x+2200ЎЭ450
ЅвµГЈє300ЎЬxЎЬ350Ј®
ЛщТФyУлxЦ®јдµДєЇКэ№ШПµКЅОЄЈєy=-5x+2200ЈЁ300ЎЬxЎЬ350Ј©Ј»
(3)ЎўW=ЈЁx-200Ј©ЈЁ-5x+2200Ј©Ј¬ ХыАнµГЈєW=-5![]() +72000Ј®
+72000Ј®
ЎЯx=320ФЪ300ЎЬxЎЬ350ДЪЈ¬ Ўаµ±x=320К±Ј¬ЧоґуЦµОЄ72000Ј¬
јґКЫјЫ¶ЁОЄ320ФЄ/МЁК±Ј¬ЙМіЎГїФВПъКЫХвЦЦїХЖшѕ»»ЇЖчЛщ»сµГµДАыИуwЧоґуЈ¬ЧоґуАыИуКЗ72000ФЄЈ®


 »ЖёФМмМмБ·їЪЛгМвїЁПµБРґр°ё
»ЖёФМмМмБ·їЪЛгМвїЁПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛД±ЯРОABCDЦРЈ¬ADЎОBCЈ¬ЎПBЈЅ90ЎгЈ¬ABЈЅ8 cmЈ¬ADЈЅ12 cmЈ¬BCЈЅ18 cmЈ¬µгPґУµгAіц·ўЈ¬ТФ1 cm/sµДЛЩ¶ИПтµгDФЛ¶ЇЈ»µгQґУµгCН¬К±іц·ўЈ¬ТФ2 cm/sµДЛЩ¶ИПтµгBФЛ¶ЇЈ®№ж¶ЁЖдЦРТ»ёц¶ЇµгµЅґп¶ЛµгК±Ј¬БнТ»ёц¶ЇµгТІЛжЦ®НЈЦ№ФЛ¶ЇЈ®ФЪХвЦЦЗйїцПВЗлДгЅвѕцТФПВОКМвЈє
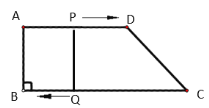
ЈЁ1Ј©ґУФЛ¶ЇїЄКјЈ¬µ±tИЎєОЦµК±Ј¬ЛД±ЯРОPQBAКЗѕШРОЈ»
ЈЁ2Ј©ФЪХыёцФЛ¶Ї№эіМЦРКЗ·сґжФЪtЦµЈ¬К№µГЛД±ЯРОPQCDКЗБвРОЈїИфґжФЪЈ¬ЗлЗуіцtЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ»
ЈЁ3Ј©ФЪХыёцФЛ¶Ї№эіМЦРКЗ·сґжФЪtЈ¬К№µГЎчDQCКЗµИСьИэЅЗРОЈїИфґжФЪЈ¬ЗлЗуіцtЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛЅвДіЦРС§![]() ГыС§ЙъјТі¤¶ФЎ°С§ЙъґшКЦ»ъЙПС§Ў±µДМ¬¶ИЈ¬ґУЦРЛж»ъµчІйБЛ
ГыС§ЙъјТі¤¶ФЎ°С§ЙъґшКЦ»ъЙПС§Ў±µДМ¬¶ИЈ¬ґУЦРЛж»ъµчІйБЛ![]() ёцјТі¤Ј¬Ѕб№ыУР
ёцјТі¤Ј¬Ѕб№ыУР![]() ёцјТі¤іЦ·ґ¶ФМ¬¶ИЈ¬ФтПВБРЛµ·ЁХэИ·µДКЗ(ЎЎЎЎ)
ёцјТі¤іЦ·ґ¶ФМ¬¶ИЈ¬ФтПВБРЛµ·ЁХэИ·µДКЗ(ЎЎЎЎ)
A.µчІй·ЅКЅКЗЖХІйB.ёГРЈЦ»УР![]() ёцјТі¤іЦ·ґ¶ФМ¬¶И
ёцјТі¤іЦ·ґ¶ФМ¬¶И
C.ёГРЈФјУР![]() µДјТі¤іЦ·ґ¶ФМ¬¶ИD.Сщ±ѕИЭБїКЗ
µДјТі¤іЦ·ґ¶ФМ¬¶ИD.Сщ±ѕИЭБїКЗ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїМеУэОД»ЇУГЖ·ЙМµк№єЅшАєЗтєНЕЕЗт№І20ёцЈ¬ЅшјЫєНКЫјЫИзПВ±нЈ¬И«ІїПъКЫНкєу№І»сАыИу260ФЄЈ®
АєЗт | ЕЕЗт | |
ЅшјЫЈЁФЄ/ёцЈ© | 80 | 50 |
КЫјЫЈЁФЄ/ёцЈ© | 95 | 60 |
ЗуЈєЈЁ1Ј©№єЅшАєЗтєНЕЕЗтёч¶аЙЩёцЈї
ЈЁ2Ј©ПъКЫ6ёцЕЕЗтµДАыИуУлПъКЫјёёцАєЗтµДАыИуПаµИЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј,ФЪЖЅГжЦ±ЅЗЧш±кПµЦР,A(aЈ¬0)Ј¬BЈЁbЈ¬0Ј©Ј¬C(-1Ј¬2)Ј¬ЗТ![]() +(a+2b-4)2=0.
+(a+2b-4)2=0.
ЈЁ1Ј©ЗуaЈ¬bµДЦµ.
ЈЁ2Ј©ФЪyЦбµДХэ°лЦбЙПґжФЪТ»µгMЈ¬К№SЎчCOM=![]() SЎчABCЈ¬ЗуіцµгMµДЧш±к.
SЎчABCЈ¬ЗуіцµгMµДЧш±к.
ЈЁ3Ј©ФЪЧш±кЦбµДЖдЛыО»ЦГКЗ·сУРФЪµгMЈ¬К№SЎчCOM=![]() SЎчABCИФіЙБўЈїИфґжФЪЈ¬ЗлЦ± ЅУРґіц·ыєПМхјюµДµгMµДЧш±к.
SЎчABCИФіЙБўЈїИфґжФЪЈ¬ЗлЦ± ЅУРґіц·ыєПМхјюµДµгMµДЧш±к.

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»ёцБгјюµДРОЧґИзНјЛщКѕЈ¬°ґ№ж¶ЁЎПAУ¦µИУЪ90ЎгЈ¬ЎПBЎўЎПDУ¦·Ц±рКЗ20ЎгєН30Ўг.
ЈЁ1Ј©АоКеКеБїµГЎПBCD=142ЎгЈ¬ёщѕЭАоКеКеБїµГµДЅб№ыЈ¬ДгДЬ¶П¶ЁХвёцБгјюКЗ·сєПёсЈїЗлЅвКНДгµДЅбВЫ.
ЈЁ2Ј©ДгЦЄµАЎПBЎўЎПDЎўЎПBCDИэЅЗЦ®јдУРєО№ШПµВрЈїЗлРґіцДгµДЅбВЫЈЁІ»РиЛµГчАнУЙЈ©.

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅв·ЅіМЈЁЧйЈ©»тІ»µИКЅЈЁЧйЈ©Іў°СµЪЈЁ4Ј©µДЅвјЇ±нКѕФЪКэЦбЙП.
ЈЁ1Ј© Ј»
Ј»
ЈЁ2Ј©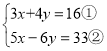 Ј»
Ј»
ЈЁ3Ј©![]() Ј»
Ј»
ЈЁ4Ј©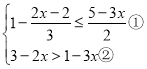 .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬RtЎчABCЦРЈ¬ЎПBAC=90ЎгЈ¬AB=ACЈ¬µгDОЄBCµДЦРµгЈ¬µгEЎўF·Ц±рФЪ±ЯABєН±ЯACЙПЈ¬ЗТЎПEDF=90ЎгЈ¬ФтПВБРЅбВЫТ»¶ЁіЙБўµДКЗ_______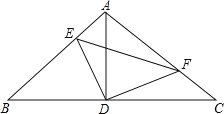
ўЩЎчADFЎХЎчBDE
ўЪSЛД±ЯРОAEDF=![]() SЎчABC
SЎчABC
ўЫBE+CF=AD
ўЬEF=AD
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄНЖ№гСф№вМеУэЎ°ґуїОјдЎ±»о¶ЇЈ¬ОТКРДіЦРС§ѕц¶ЁФЪС§ЙъЦРїЄЙиAЈєКµРДЗтЈ¬BЈєБў¶ЁМшФ¶Ј¬CЈєМшЙюЈ¬DЈєЕЬІЅЛДЦЦ»о¶ЇПоДїЈ®ОЄБЛБЛЅвС§Йъ¶ФЛДЦЦПоДїµДПІ»¶ЗйїцЈ¬Лж»ъійИЎБЛІї·ЦС§ЙъЅшРРµчІйЈ¬ІўЅ«µчІйЅб№ы»жЦЖіЙИзНјўЩўЪµДНіјЖНјЈ®ЗлЅбєПНјЦРµДРЕПўЅвґрПВБРОКМвЈє
ЈЁ1Ј©ФЪХвПоµчІйЦРЈ¬№ІµчІйБЛ¶аЙЩГыС§ЙъЈї
ЈЁ2Ј©ЗлјЖЛг±ѕПоµчІйЦРПІ»¶Ў°Бў¶ЁМшФ¶Ў±µДС§ЙъИЛКэєНЛщХј°Щ·Ц±ИЈ¬ІўЅ«БЅёцНіјЖНјІ№ідНкХыЈ»
ЈЁ3Ј©ИфµчІйµЅПІ»¶Ў°МшЙюЎ±µД5ГыС§ЙъЦРУР3ГыДРЙъЈ¬2ГыЕ®ЙъЈ®ПЦґУХв5ГыС§ЙъЦРИОТвійИЎ2ГыС§ЙъЈ®ЗлУГ»КчЧґНј»тБР±нµД·Ѕ·ЁЈ¬ЗуіцёХєГійµЅН¬РФ±рС§ЙъµДёЕВКЈ®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com