
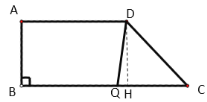
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B��90����AB��8 cm��AD��12 cm��BC��18 cm����P�ӵ�A��������1 cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������2 cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶���������������������������⣺
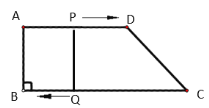
��1�����˶���ʼ����tȡ��ֵʱ���ı���PQBA�Ǿ��Σ�
��2���������˶��������Ƿ����tֵ��ʹ���ı���PQCD�����Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
��3���������˶��������Ƿ����t��ʹ����DQC�ǵ��������Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
���𰸡���1��6����2�������ڣ����������������3�����ڣ���t��5��6��![]() ʱ����DQC�ǵ��������Σ�
ʱ����DQC�ǵ��������Σ�
��������
��1�������⣬��AP��t��DP��12��t��CQ��2t��BQ��18��2t���ٸ��ݾ��ε��ж����м��㼴�ɵõ��𰸣�
��2��Ҫʹ�ı���PQCD�����Σ����ı���PQCDһ����ƽ���ı��Σ�������֪��t��4ʱ���ı���PQCD��ƽ���ı��Σ���DP��12��t��8��10����DP��DC�����������ε��ж��õ��𰸣�
��3��������������ۣ��ٵ�QC��DCʱ����2t��10����t��5��
�ڵ�DQ��DCʱ������D��DH��CQ���ɹ��ɶ����õ�DC��10����t��6��
�۵�QD��QCʱ������D��DH��CQ����Rt��DQH�У�DH2��QH2��DQ2������õ�t��![]() ��
��
�⣺��1����ͼ�������⣬��AP��t��DP��12��t��CQ��2t��BQ��18��2t��
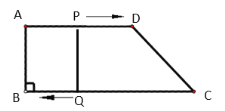
Ҫʹ�ı���PQBA�Ǿ��Σ�������B��90����AD��BC����AP��BQ��ֻ������AP��BQ����t��18��2t�����t��6��
���Ե�t��6ʱ���ı���PQBA�Ǿ��Σ�
��2�������ڣ����ɣ�
Ҫʹ�ı���PQCD�����Σ����ı���PQCDһ����ƽ���ı��Σ�
����֪��t��4ʱ���ı���PQCD��ƽ���ı��Σ�
��ʱDP��12��t��8��10����DP��DC��
������֪�ٶ��˶����ı���PQCDֻ����ƽ���ı��Σ��������������Σ�
��3����DQC�ǵ���������ʱ��������������ۣ�
����ͼ1����QC��DCʱ����2t��10����t��5��
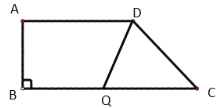
ͼ1
����ͼ2����DQ��DCʱ������D��DH��CQ��
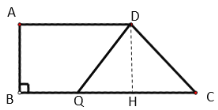
ͼ2
��QH��CH��![]() CQ��t��
CQ��t��
��Rt��DHC��DH��8��CH��BC��AD��6��
��DC��![]() ��10��
��10��
��t��6��
����ͼ3����QD��QCʱ������D��DH��CQ��
ͼ3
DH��8��CH��6��DC��10��CQ��QD��2t��QH��|2t��6|��
��Rt��DQH��DH2��QH2��DQ2��
��82��|2t��6|2��(2t)2��
���t��![]() ��
��
���ϣ���t��5��6��![]() ʱ����DQC�ǵ��������Σ�
ʱ����DQC�ǵ��������Σ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2tx+t2��2t+4��0��
��1����t��3ʱ����������̣�
��2����m��n�Ƿ��̵�����ʵ��������Q����m��2����n��2��������Q����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() �У�
��![]() ��
��![]() ���е㣬
���е㣬![]() ������Ϊ
������Ϊ![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
��1����![]() �Ķ�����
�Ķ�����
��2����![]() ,
,![]() ����
����![]() �ij���
�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����AD��BC����O�㣬���ݡ��������ڽǺ���180�㡱�����ѵó������������еĽǴ������¹�ϵ������DOC����AOB������D+��C����A+��B��
��������⣩
�ֱ�������BAD�͡�BCD��ƽ���ߣ�������ƽ���߽��ڵ�E����ͼ��2������E���D����B֮���Ƿ����ij��������ϵ�أ�
��������⣩
Ϊ�˽����������⣬�����ȴӼ������������ʼ̽����
��֪��BAD��ƽ�������BCD��ƽ���߽��ڵ�E��
��1����ͼ��3������AB��CD����D��30�㣬��B��40�㣬���E���� ����
��2����ͼ��4������AB��ƽ��CD����D��30�㣬��B��50�㣬���E�Ķ����Ƕ����أ�
С��������˼���ģ������������������̣�
��֤��D+��1����E+��3����B+��4����E+��2��
���D+��1+��B+��4���� ����
��CE��AE�ֱ��ǡ�BCD����BAD��ƽ���ߣ�
���1����2����3����4��
��2��E���� ����
�֡ߡ�D��30�㣬��B��50�㣬
���E���� ���ȣ�
��3�����ܽ�ǰ���ʵĻ����ϣ�����ͼ��2����ֱ��д����E���D����B֮���������ϵ�ǣ��� ����
�����Ӧ�ã�
��ͼ��5������BAD��ƽ����AE���BCD��ƽ����CE���ڵ�E��
��֪����D��m�㡢��B��n�㣬��m��n����E�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
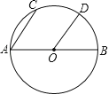
����Ŀ����ͼ����֪AB����O��ֱ������AC��OD.
��1����֤��![]() ��
��
��2����![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ������AOD�Ķ�����
������AOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ʮ�ߴ�����������ij��У�ʵ�ֿ�Խʽ��չ��������������������Ͷ�ʼƻ������ƽ������·������Ҫ������ʯ�����ƻ�ÿСʱ�ھ���ʯ��270m3���־�����ij���ͻ�е����˾���üס��������ͺŵ��ھ������������������˾�ṩ���ھ���й���Ϣ�����
��𣨵�λ��Ԫ/̨ʱ�� | �ھ���ʯ��������λ��m3/̨ʱ�� | |
�����ھ�� | 200 | 30 |
�����ھ�� | 260 | 40 |
��1�������üס��������ͺŵ��ھ����8̨��ǡ�����ÿСʱ���ھ�������ס��������ͺŵ��ھ���������̨��
��2�����ÿСʱ֧���������1780Ԫ����ǡ�����ÿСʱ���ھ�������ô���м��ֲ�ͬ�����÷�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ÿ��2�M���ٶ���ͼ�ı߿�![]() ��·���ƶ�,��Ӧ����ABP�����S����ʱ��t�ĺ���ͼ����ͼ��.��AB=6,�Իش��������⣺
��·���ƶ�,��Ӧ����ABP�����S����ʱ��t�ĺ���ͼ����ͼ��.��AB=6,�Իش��������⣺

(1)ͼ���е�BC���Ƕ��٣�
(2)ͼ���е�a�Ƕ���?
(3)ͼ���е�ͼ������Ķ���?
(4)ͼ����b�Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ��п��������ԣ��ס��ҡ�����λͬѧ����������ѵ�������һ���˽������������һ���˽��£���ÿλ�����˴����������˵Ļ����Ǿ��ȵģ��ɼ�ʼ�����������Σ�
��1����������״ͼ�оٳ����δ�������п��������
��2�������δ������ص����µĸ��ʣ�
��3�����δ������ص����µĸ��ʴ��Ǵ����ҽ��µĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com