
����Ŀ����ͼ��1����AD��BC����O�㣬���ݡ��������ڽǺ���180�㡱�����ѵó������������еĽǴ������¹�ϵ������DOC����AOB������D+��C����A+��B��
��������⣩
�ֱ�������BAD�͡�BCD��ƽ���ߣ�������ƽ���߽��ڵ�E����ͼ��2������E���D����B֮���Ƿ����ij��������ϵ�أ�
��������⣩
Ϊ�˽����������⣬�����ȴӼ������������ʼ̽����
��֪��BAD��ƽ�������BCD��ƽ���߽��ڵ�E��
��1����ͼ��3������AB��CD����D��30�㣬��B��40�㣬���E���� ����
��2����ͼ��4������AB��ƽ��CD����D��30�㣬��B��50�㣬���E�Ķ����Ƕ����أ�
С��������˼���ģ������������������̣�
��֤��D+��1����E+��3����B+��4����E+��2��
���D+��1+��B+��4���� ����
��CE��AE�ֱ��ǡ�BCD����BAD��ƽ���ߣ�
���1����2����3����4��
��2��E���� ����
�֡ߡ�D��30�㣬��B��50�㣬
���E���� ���ȣ�
��3�����ܽ�ǰ���ʵĻ����ϣ�����ͼ��2����ֱ��д����E���D����B֮���������ϵ�ǣ��� ����
�����Ӧ�ã�
��ͼ��5������BAD��ƽ����AE���BCD��ƽ����CE���ڵ�E��
��֪����D��m�㡢��B��n�㣬��m��n����E�Ķ�����

���𰸡���������⡿��1��35�㣻��2��2��E+��3+��2����D+��B��40�㣻��3����E��![]() �������Ӧ�á���E��
�������Ӧ�á���E��![]() ��n��m���㣮
��n��m���㣮
��������
������⣺��1���������������ε���һ�ԶԶ�����ȵã���D+��DCE����E+��DAE����E+��ECB����B+��EAB����ʽ��Ӻ��ٸ��ݽ�ƽ���ߵĶ���ɵý��ۣ�
��2��ͬ������ʽ��ӿɵý��ۣ�
��3�����ݣ�1���ͣ�2���ɵý��ۣ�
���Ӧ�ã������ӳ�BC��AD�ڵ�F������������ǵ����ʣ��ɵá�BCD����B+��BAD+��D�����ɽ�ƽ���ߵ����ʣ�������ô𰸣�
������⣺��1����ͼ3���ߡ�D+��DCE����E+��DAE��
��E+��ECB����B+��EAB��
���D+��DCE+��B+��EAB��2��E+��DAE+��ECB��
��ECƽ�֡�ECB��AEƽ�֡�BAD��
���DCE����ECB����DAE����BAE��
��2��E����B+��D��
���E��![]()
���E��![]() ��30��+40������
��30��+40������![]() ��70����35����
��70����35����
�ʴ�Ϊ��35����
��2����ͼ��4������D+��1����E+��3����B+��4����E+��2��
���D+��1+��B+��4��2��E+��3+��2��
��CE��AE�ֱ��ǡ�BCD����BAD��ƽ���ߣ�
���1����2����3����4��
��2��E����D+��B��
���E��![]() ��
��
�֡ߡ�D��30������B��50����
���E��40�ȣ�
�ʴ�Ϊ��2��E+��3+��2����D+��B��40����
��3���ɣ�1���ͣ�2���ã���E��![]() ��
��
�ʴ�Ϊ����E��![]() ��
��
���Ӧ��:
��ͼ��5�����ӳ�BC��AD��F��
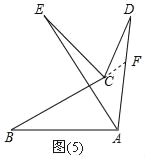
�ߡ�BFD����B+��BAD��
���BCD����BFD+��D����B+��BAD+��D��
��CEƽ�֡�BCD��AEƽ�֡�BAD
���ECD����ECB��![]() ��BCD����EAD����EAB��
��BCD����EAD����EAB��![]() ��BAD��
��BAD��
�ߡ�E+��ECB����B+��EAB��
���E����B+��EAB����ECB����B+��BAE��![]() ��BCD����B+��BAE��
��BCD����B+��BAE��![]() ����B+��BAD+��D����
����B+��BAD+��D����![]() ����B����D����
����B����D����
�ߡ�D��m������B��n����
����E��![]() ��n��m������
��n��m������


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У���A(o,m),��B(n,0)��m, n����![]() .
.
(1)��A,B������.
(2)��ͼ1, EΪ�ڶ�������ֱ��AB�ϵ�һ�㣬������![]() �����E�ĺ�����.
�����E�����.
(3)��ͼ2,ƽ���߶�BA��OC, B��O�Ƕ�Ӧ�㣬A��C�Ƕ�Ӧ�㣬����AC, EΪBA���ӳ�����һ�㣬����EO, OFƽ�֡�COE, AFƽ�֡�EAC, OF��AF�ڵ�F,����ABO+��OEB=��,����ͼ2�н�ͼ�β��������������F (�ú�����ʽ�ӱ�ʾ)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
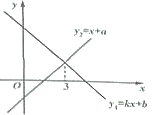
����Ŀ����֪һ�κ���![]() ��
��![]() ͼ����ͼ��ʾ�������н��ۣ���
ͼ����ͼ��ʾ�������н��ۣ���![]() ����
����![]() ���۹���
���۹���![]() �ķ���
�ķ���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ���ܵ�
���ܵ�![]() ��
��![]() .������ȷ����_______(�����)��
.������ȷ����_______(�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������3��1��
��1������ͼ��ʾ�������ϣ��ֱ���A��B��ʾ����3��1�������㣻
��2����|m|��2�������ϱ�ʾm�ĵ���ڵ�A��B֮�䣻�ڵ�A�Ҳ��ҵ���B����Ϊ5�ĵ��ʾ����Ϊn�������x�IJ���ʽmx+4��n�����ѽ⼯��ʾ����ͼ��ʾ�������ϣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ţ�̣�����Ϊÿ��24Ԫ���涨�ۼ۲����ڽ��ۣ����ڵ��ۼ�Ϊÿ��36Ԫ��ÿ�¿�����60�䣮�г����鷢�֣�������ţ�̵��ۼ�ÿ����1Ԫ����ÿ�µ�����������10�䣬��ÿ��ţ�̽���xԪ(xΪ������)��ÿ�µ�����Ϊy�䣮
��1��д��y��x�м�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������ζ��ۣ�����ʹÿ������ţ�̵����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��4��29��������̲�����ˡ�����������λ�֡����飬�������飬���ּ�ͥ���顱�������̣����С����ּ�ͥ���顱������ֻͥ���ԡ�����һС����һ��һС������ʽ�μӣ�����������100��.
��1�����μӡ����ּ�ͥ���顱�Ĵ���������С��������1.5�����ʣ�������һС���͡�һ��һС���������ֱ��м��飿
��2����������һС���͡�һ��һС������������ͬ��������5�飬�α����вμ� �����ּ�ͥ���顱���� �飨ֱ��д���𰸣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B��90����AB��8 cm��AD��12 cm��BC��18 cm����P�ӵ�A��������1 cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������2 cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶���������������������������⣺
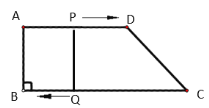
��1�����˶���ʼ����tȡ��ֵʱ���ı���PQBA�Ǿ��Σ�
��2���������˶��������Ƿ����tֵ��ʹ���ı���PQCD�����Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
��3���������˶��������Ƿ����t��ʹ����DQC�ǵ��������Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
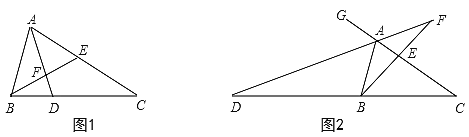
����Ŀ����ͼ,����ABC��,��E��AC��,��AEB=��ABC.
(1)ͼ1��,����BAC�Ľ�ƽ����AD,�ֱ�CB��BE��D��F����,��֤:��EFD=��ADC��
(2)ͼ2��,����ABC�������BAG�Ľ�ƽ����AD,�ֱ�CB��BE���ӳ�����D��F����,��̽��(1)�н����Ƿ��Գ���?Ϊʲô?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ļ���Ʒ�̵깺�����������20�������ۺ��ۼ����±���ȫ�������������260Ԫ��
���� | ���� | |
���ۣ�Ԫ/���� | 80 | 50 |
�ۼۣ�Ԫ/���� | 95 | 60 |
����1�������������������ٸ���
��2������6����������������ۼ��������������ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com