Question

【题目】已知，在平面直角坐标系中，点A(o,m),点B(n,0)，m, n满足.

(1)求A,B的坐标.

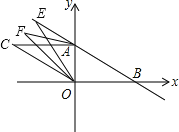
(2)如图1, E为第二象限内直线AB上的一点，且满足，求点E的横坐标.

(3)如图2,平移线段BA至OC, B与O是对应点，A与C是对应点，连接AC, E为BA的延长线上一点，连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整，并求∠F (用含α的式子表示)

Answer 1

【答案】（1）A(0,3),B(4,0);（2）;（3）

【解析】

（1）根据非负数的性质列式求出m、n的值，然后写出点A、B的坐标即可；

（2）设点E的横坐标为a，然后利用三角形的面积列式求出a的值，再利用待定系数法求出直线AB的解析式，然后求解即可；

（3）根据平移的性质可得AB∥OC，AC∥OB，根据平行线的性质可得∠OEB=∠COE，∠CAE=∠ABO，然后根据角平分线的定义可得，，再根据三角形的内角和定理列式整理即可得解．

解：（1）由非负数的性质得，m-3=0，n-4=0，

解得m=3，n=4，

所以，A（0，3）B（4，0）；

（2）设点E的横坐标为a，

，

，

解得a=，

设直线AB的解析式为y=kx+b，

则

解得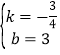

所以，直线AB的解析式为，

当时，，

所以，点E的坐标为；

（3）由平移的性质，AB∥OC，AC∥OB，

∴∠OEB=∠COE，∠CAE=∠ABO，

∵OF平分∠COE，AF平分∠EAC，

，

由三角形的内角和定理，∠OEB+∠EAF=∠F+∠EOF，

，

，

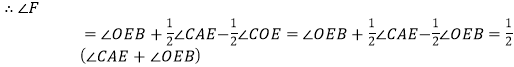∵∠ABO+∠OEB=α，

.