练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

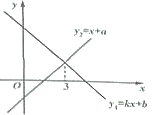
    【题目】已知一次函数与图象如图所示，则下列结论：①；②；③关于的方程的解为；④当，.其中正确的有_______(填序号)．

    【答案】③④

    【解析】

    根据一次函数的性质对①②进行判断；利用一次函数与一元一次方程的关系对③进行判断；利用函数图象，当x＞3时，一次函数y1=kx+b在直线y2=x+a的下方，则可对④进行判断．

    解：∵一次函数y1＝kx+b经过第一、二、四象限，

    ∴k＜0，b＞0，所以①错误；

    ∵直线y2＝x+a的图象与y轴的交点在x轴，下方，

    ∴a＜0，所以②错误；

    ∵一次函数y1＝kx+b与y2＝x+a的图象的交点的横坐标为3，

    ∴x＝3时，kx+b＝x﹣a，所以③正确；

    当x＞3时，y1＜y2，所以④正确．

    故答案为③④．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读理解：用“十字相乘法”分解因式2x2﹣x﹣3的方法．
    （i）二次项系数2=1×2；
    （ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；

    1×3+2×（﹣1）=1 1×（﹣1）+2×3=5 1×（﹣3）+2×1=﹣1 1×1+2×（﹣3）=﹣5
    （iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．
    即：（x+1）（2x﹣3）=2x2﹣3x+2x﹣3=2x2﹣x﹣3，则2x2﹣x﹣3=（x+1）（2x﹣3）．
    像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2+5x﹣12= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4＝0．

    （1）当t＝3时，解这个方程；

    （2）若m，n是方程的两个实数根，设Q＝（m﹣2）（n﹣2），试求Q的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某气象台发现：在某段时间里，如果早晨下雨，那么晚上是晴天；如果晚上下雨，那么早晨是晴天，已知这段时间有9天下了雨，并且有6天晚上是晴天，7天早晨是晴天，则这一段时间有（ ）
    A.9天
    B.11天
    C.13天
    D.22天

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某家电商场计划用9万元从生产厂家购进50台电视机．已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．
    （1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案；
    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.

    （1）求每台电脑、每台电子白板各多少万元?

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在中，是的中点，，垂足为，交于点，且．

    （1）求的度数；

    （2）若,，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），AD，BC交于O点，根据“三角形内角和是180°”，不难得出两个三角形中的角存在以下关系：①∠DOC＝∠AOB；②∠D+∠C＝∠A+∠B．

    （提出问题）

    分别作出∠BAD和∠BCD的平分线，两条角平分线交于点E，如图（2），∠E与∠D、∠B之间是否存在某种数量关系呢？

    （解决问题）

    为了解决上面的问题，我们先从几个特殊情况开始探究．

    已知∠BAD的平分线与∠BCD的平分线交于点E．

    （1）如图（3），若AB∥CD，∠D＝30°，∠B＝40°，则∠E＝　 　．

    （2）如图（4），若AB不平行CD，∠D＝30°，∠B＝50°，则∠E的度数是多少呢？

    小明是这样思考的，请你帮他完成推理过程：

    易证∠D+∠1＝∠E+∠3，∠B+∠4＝∠E+∠2，

    ∴∠D+∠1+∠B+∠4＝　 　，

    ∵CE、AE分别是∠BCD、∠BAD的平分线，

    ∴∠1＝∠2，∠3＝∠4．

    ∴2∠E＝　 　，

    又∵∠D＝30°，∠B＝50°，

    ∴∠E＝　 　度．

    （3）在总结前两问的基础上，借助图（2），直接写出∠E与∠D、∠B之间的数量关系是：　 　．

    （类比应用）

    如图（5），∠BAD的平分线AE与∠BCD的平分线CE交于点E．

    已知：∠D＝m°、∠B＝n°，（m＜n）求：∠E的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了参加中考体育测试，甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给其余两人的机会是均等的，由甲开始传球，共传球三次．

    （1）请利用树状图列举出三次传球的所有可能情况；

    （2）求三次传球后，球回到甲脚下的概率；

    （3）三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？

    查看答案和解析>>

    同步练习册答案