
����Ŀ��Ϊ�˽�ʮ�ߴ�����������ij��У�ʵ�ֿ�Խʽ��չ��������������������Ͷ�ʼƻ������ƽ������·������Ҫ������ʯ�����ƻ�ÿСʱ�ھ���ʯ��270m3���־�����ij���ͻ�е����˾���üס��������ͺŵ��ھ������������������˾�ṩ���ھ���й���Ϣ�����
��𣨵�λ��Ԫ/̨ʱ�� | �ھ���ʯ��������λ��m3/̨ʱ�� | |
�����ھ�� | 200 | 30 |
�����ھ�� | 260 | 40 |
��1�������üס��������ͺŵ��ھ����8̨��ǡ�����ÿСʱ���ھ�������ס��������ͺŵ��ھ���������̨��
��2�����ÿСʱ֧���������1780Ԫ����ǡ�����ÿСʱ���ھ�������ô���м��ֲ�ͬ�����÷�����
���𰸡���1���ס��������ͺŵ��ھ������5̨��3̨����2���������ֲ�ͬ�����÷�����
��������
��1��������������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ����Խ���⣻
��2��������������г���Ӧ�IJ���ʽ��ע����ҵ�̨������������
��1����ס��������ͺŵ��ھ������x̨��y̨��
![]() ��
��
��![]() ��
��
�𣺼ס��������ͺŵ��ھ������5̨��3̨��
��2�������ü��ͺŵ��ھ��ą���������ͺŵ��ھ��b̨��
![]() ��
��
��ã�a��5��
��a��5ʱ��b��3��
��a��4ʱ��b��![]() ����ȥ����
����ȥ����
��a��3ʱ��b��![]() ����ȥ����
����ȥ����
��a��2ʱ��b��![]() ����ȥ����
����ȥ����
��a��1ʱ��b��6��
��a��0ʱ��b��![]() ����ȥ����
����ȥ����
�𣺹������ֲ�ͬ�����÷�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У�AD��BC��Ҫ�б��ı���ABCD��ƽ���ı��Σ��������������� ��
A. ��A+��C=180��B. ��B+��D=180��
C. ��A+��B=180��D. ��A+��D=180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������3��1��
��1������ͼ��ʾ�������ϣ��ֱ���A��B��ʾ����3��1�������㣻
��2����|m|��2�������ϱ�ʾm�ĵ���ڵ�A��B֮�䣻�ڵ�A�Ҳ��ҵ���B����Ϊ5�ĵ��ʾ����Ϊn�������x�IJ���ʽmx+4��n�����ѽ⼯��ʾ����ͼ��ʾ�������ϣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��4��29��������̲�����ˡ�����������λ�֡����飬�������飬���ּ�ͥ���顱�������̣����С����ּ�ͥ���顱������ֻͥ���ԡ�����һС����һ��һС������ʽ�μӣ�����������100��.
��1�����μӡ����ּ�ͥ���顱�Ĵ���������С��������1.5�����ʣ�������һС���͡�һ��һС���������ֱ��м��飿
��2����������һС���͡�һ��һС������������ͬ��������5�飬�α����вμ� �����ּ�ͥ���顱���� �飨ֱ��д���𰸣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B��90����AB��8 cm��AD��12 cm��BC��18 cm����P�ӵ�A��������1 cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������2 cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶���������������������������⣺
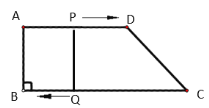
��1�����˶���ʼ����tȡ��ֵʱ���ı���PQBA�Ǿ��Σ�
��2���������˶��������Ƿ����tֵ��ʹ���ı���PQCD�����Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
��3���������˶��������Ƿ����t��ʹ����DQC�ǵ��������Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ��ȤС���У�С��������ͬ�����Ե�Բ�ܽǼ�Բ�Ľǵ�������̽����һЩ���⣬���������С��һ�����̽��֮�ã�
�����龳��
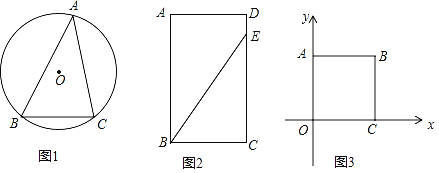
��1����ͼ1������ABC�У���A=30����BC=2������ABC�����Բ�İ뾶Ϊ�� ����
����ʵ����
��2����ͼ2���ھ���ABCD�У����������ϲ�������õľ��飬�ھ���ABCD�ڲ���ֱ����Բ������һ��P����P���㣺��BPC=��BEC����PB=PC����Ҫ����ֱ����Բ��������P��������ͼ�ۼ�����
Ǩ��Ӧ�ã�
��3����ͼ3����ƽ��ֱ������ϵ�ĵ�һ��������һ��B������Ϊ��2��m��������B��AB��y�ᣬBC��x�ᣬ����ֱ�ΪA��C������P���߶�AB�ϻ�������P�������A��B�غϣ�������ʹ�á�OPC=45����λ������������m��ȡֵ��ΧΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
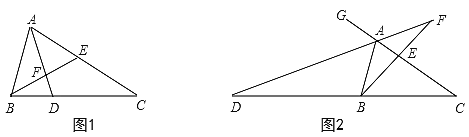
����Ŀ����ͼ,����ABC��,��E��AC��,��AEB=��ABC.
(1)ͼ1��,����BAC�Ľ�ƽ����AD,�ֱ�CB��BE��D��F����,��֤:��EFD=��ADC��
(2)ͼ2��,����ABC�������BAG�Ľ�ƽ����AD,�ֱ�CB��BE���ӳ�����D��F����,��̽��(1)�н����Ƿ��Գ���?Ϊʲô?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1��O�ǵȱ���ABC��һ�㣬����OA��OB��OC����OA=3��OB=4��OC=5������BAO�Ƶ�B˳ʱ����ת��õ���BCD������OD����

����ת�ǵĶ�����
���߶�OD�ij���
�ۡ�BDC�Ķ�����
��2����ͼ2��ʾ��O�ǵ���ֱ����ABC����ABC=90������һ�㣬����OA��OB��OC������BAO�Ƶ�B˳ʱ����ת��õ���BCD������OD����OA��OB��OC����ʲô����ʱ����ODC=90���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������״��ͼ��ʾ�����涨��AӦ����90������B����DӦ�ֱ���20����30��.
��1�����������á�BCD=142�����������������õĽ�������ܶ϶��������Ƿ�ϸ��������Ľ���.
��2����֪����B����D����BCD����֮���кι�ϵ����д����Ľ��ۣ�����˵�����ɣ�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com