【题目】四边形ABCD中，AD∥BC，要判别四边形ABCD是平行四边形，还需满足条件（ ）

A. ∠A+∠C=180°B. ∠B+∠D=180°

C. ∠A+∠B=180°D. ∠A+∠D=180°

参考答案：

【答案】D

【解析】

四边形ABCD中，已经具备AD∥BC，再根据选项，选择条件，推出AB∥CD即可，只有D选项符合．

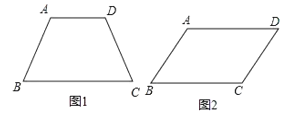
解：A、如图1，∵AD∥BC，

∴∠A＋∠B＝180°，

如果∠A＋∠C＝180°，

则可得：∠B＝∠C，

这样的四边形是等腰梯形，不是平行四边形，故此选项错误；

B、如图1，∵AD∥BC，

∴∠A＋∠B＝180°，

如果∠B＋∠D＝180°，

则可得：∠A＝∠D，

这样的四边形是等腰梯形，不是平行四边形，故此选项错误；

C、如图1，∵AD∥BC，

∴∠A＋∠B＝180°，

再加上条件∠A＋∠B＝180°，

也证不出四边形ABCD是平行四边形，故此选项错误；

D、如图2，

∵∠A＋∠D＝180°，

∴AB∥CD，

∵AD∥BC，

∴四边形ABCD是平行四边形，故此选项正确；

故选：D．

关闭