
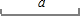
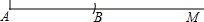
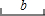

| 1 |
| 2 |
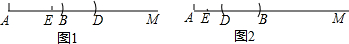


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:阅读理解
(本题14分)阅读:在用尺规作线段![]() 等于线段
等于线段![]() 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段![]() .
. ![]()
![]() 求作:线段
求作:线段![]() ,使得线段
,使得线段![]() .
.
作法: ① 作射线![]() ;
;
② 在射线![]() 上截取
上截取![]() .
.
∴线段![]() 为所求.
为所求.
解决下列问题:已知:如图,线段![]() .
. ![]()
(1)请你仿照小明的作法,在上图中的射线![]() 上作线段
上作线段![]() ,使得
,使得![]() ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取![]() 的中点
的中点![]() .若
.若![]() .
.
①当点![]() 在线段
在线段![]() 上时(画出图形)。段
上时(画出图形)。段![]() 的长.
的长.
②当点![]() 在线段
在线段![]() 的延长线上时(画出图形). 求线段
的延长线上时(画出图形). 求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2012-2013年湖北省十堰市七年级上学期期末调研考试数学试卷(带解析) 题型:解答题
阅读:在用尺规作线段 等于线段
等于线段 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段 .
. 
求作:线段 ,使得线段
,使得线段 .
.
作法: ① 作射线 ;
;
② 在射线 上截取
上截取 .
.
∴线段 为所求.
为所求.
解决下列问题:
已知:如图,线段 .
. 
(1)请你仿照小明的作法,在上图中的射线 上作线段
上作线段 ,使得
,使得 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取 的中点
的中点 .若
.若 ,求线段
,求线段 的长.(要求:第(2)问重新画图解答)
的长.(要求:第(2)问重新画图解答)
查看答案和解析>>
科目:初中数学 来源:2015届湖北省十堰市七年级上学期期末调研考试数学试卷(解析版) 题型:解答题
阅读:在用尺规作线段 等于线段
等于线段 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段 .
. 
求作:线段 ,使得线段
,使得线段 .
.
作法: ① 作射线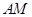 ;
;
② 在射线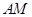 上截取
上截取 .
.
∴线段 为所求.
为所求.

解决下列问题:
已知:如图,线段 .
. 
(1)请你仿照小明的作法,在上图中的射线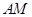 上作线段
上作线段 ,使得
,使得 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取 的中点
的中点 .若
.若 ,求线段
,求线段 的长.(要求:第(2)问重新画图解答)
的长.(要求:第(2)问重新画图解答)
查看答案和解析>>
科目:初中数学 来源:2011-2012贵州省桐梓县七年级上学期期末考试数学卷 题型:选择题
(本题14分)阅读:在用尺规作线段 等于线段
等于线段 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段 .
. 
 求作:线段
求作:线段 ,使得线段
,使得线段 .
.
作法: ① 作射线 ;
;
② 在射线 上截取
上截取 .
.
∴线段 为所求.
为所求.
解决下列问题:已知:如图,线段 .
. 
(1)请你仿照小明的作法,在上图中的射线 上作线段
上作线段 ,使得
,使得 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取 的中点
的中点 .若
.若 .
.
①当点 在线段
在线段 上时(画出图形)。段
上时(画出图形)。段 的长.
的长.
②当点 在线段
在线段 的延长线上时(画出图形). 求线段
的延长线上时(画出图形). 求线段 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com