
| x(元) | … | 20 | 22 | 25 | … |
| y(件) | … | 20 | 18 | 15 | … |
分析 (1)已知日销售量y是销售价x的一次函数,可设函数关系式为y=kx+b(k,b为常数,且k≠0),代入两组对应值求k、b,确定函数关系式.
(2)把x=28代入函数式求y,根据:(售价-进价)×销售量=利润,求解.
解答 解:(1)设此一次函数解析式为y=kx+b(k,b为常数,且k≠0),
则$\left\{\begin{array}{l}{20=20k+b}\\{15=25k+b}\end{array}\right.$,
解得k=-1,b=40,
即一次函数解析式为y=-x+40;
(2)当x=28时,每日的销售量为y=-28+40=12(件),
每日所获销售利润为(28-16)×12=144(元).
点评 本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
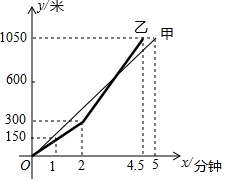 百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛,甲、乙两只龙舟队在比赛时路程y(m)与时间x(min)之间的函数图象如图所示,根据图象回答下列问题:
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛,甲、乙两只龙舟队在比赛时路程y(m)与时间x(min)之间的函数图象如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m>0)与x轴的交点为A,B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
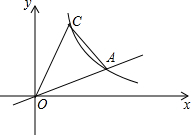 如图所示,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于点A,且点A的横坐标为4
如图所示,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于点A,且点A的横坐标为4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
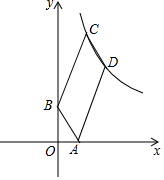 如图,已知四边形ABCD是平行四边形,AD=2AB,A,B两点的坐标分别为
如图,已知四边形ABCD是平行四边形,AD=2AB,A,B两点的坐标分别为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com