
【题目】小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第![]() 回到家中.设小明出发第
回到家中.设小明出发第![]() 时的速度为
时的速度为![]() ,离家的距离为
,离家的距离为![]() ,
,![]() 与
与![]() 之间的函数关系如图所示(图中的空心圈表示不包含这一点).
之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第![]() 时离家的距离为______m;
时离家的距离为______m;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)直接写出![]() 与
与![]() 之间的函数关系式并画出图象.
之间的函数关系式并画出图象.

【答案】(1)200;(2)s=160t120(2<t≤5);(3)S= ,函数图像见解析
,函数图像见解析
【解析】
(1)根据路程=速度×时间求出小明出发第2min时离家的距离即可;
(2)当2<t≤5时,离家的距离s=前面2min走的路程加上后面(t2)min走过的路程列式即可;
(3)根据小明是往返用了16分钟,往返的路程是一样的,根据往返路程相等,计算出的6.25min时小明开始往回走,再分类讨论:0≤t≤2、2<t≤5、5<t≤6.25和6.25<t≤16四种情况,画出各自的图形即可求解.
(1)100×2=200(m).
故小明出发第2min时离家的距离为200m;
故答案为:200.
(2)当2<t≤5时,s=100×2+160(t2)=160t120.
故s与t之间的函数表达式为s=160t120(2<t≤5);
(3)设x分钟时,小明开始往回走
依题意可得100×2+160×(5-2)+80×(x-5)=80×(16-x)
解得x=6.25
当t=6.25时,s=100×2+160×(5-2)+80×(6.25-5)=780
∴当5<t≤6.25时,s=100×2+160×(5-2)+80×(t-5)=80t+280
当6.25<t≤16时,s=780-80×(t-6.25)=128080t
∴s与t之间的函数关系式为S= ,
,
故函数图像如图如下:



 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(不与点A重合),∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着x的变化而变化?若变化,用含x的代数式表示CD的长度;若不变化,求出线段CD的长度;
(2)△PBC的面积是否存在最小值?若存在,请求出这个最小值,并求出此时的x的值;若不存在,请说明理由;
(3)当x取何值时,△ABP和△CDP相似; ![]()
(4)如图2,当以C为圆心,以CP为半径的圆与线段AB有公共点时,求x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() 的面积为
的面积为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC, ![]() ,AD=6,BC=8,
,AD=6,BC=8, ![]() ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).

(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论: ①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中描出下列各点:A(3,0),B(-4,3),C(-4, -2),并解答:
(1)点A到原点O的距离是 个单位长度;
(2)将点B向下平移__________个单位,它会与点C重合;
(3)连接BC,直线BC与y轴的位置关系是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论: ①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
A.①②③
B.③④⑤
C.①②④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
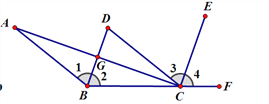
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com