
【题目】如图1,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(不与点A重合),∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着x的变化而变化?若变化,用含x的代数式表示CD的长度;若不变化,求出线段CD的长度;
(2)△PBC的面积是否存在最小值?若存在,请求出这个最小值,并求出此时的x的值;若不存在,请说明理由;
(3)当x取何值时,△ABP和△CDP相似; ![]()
(4)如图2,当以C为圆心,以CP为半径的圆与线段AB有公共点时,求x的值。
【答案】
(1)解:CD的长度不变化,理由如下:
如图1,延长CB和PA,记交点为点Q.
![]() ,
, ![]() ,
,![]() (等腰三角形“三合一”的性质).
(等腰三角形“三合一”的性质).![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
即CD=8 。
(2)解:如图2,过点B作 ![]() ,垂足为F.
,垂足为F.
![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,即CP最小值为8,
,即CP最小值为8, ![]() 面积的最小值
面积的最小值 ![]()
此时 ![]() 是等腰三角形,AP=AB=4 ,即x=4;
是等腰三角形,AP=AB=4 ,即x=4;
(3)解:当 ![]() 时,
时, ![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
即 ![]() ,
,
如图3,当
![]() 时,
时,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
即 ![]() ,
,
所以当 ![]() 或
或 ![]() 时,
时, ![]() 和
和 ![]() 相似。
相似。
(4)解:如图延长CB和PA相交于点E,
当点A在圆C上时,由(1)及垂径定理得
AE=AD=DP= ![]() x
x
由 ![]() 得
得![]()
∴ ![]()
∴x的取值范围是 ![]()
【解析】(1)CD的长度不变化,理由如下:如图1,延长CB和PA,记交点为点Q.根据等腰△QPC“三合一”的性质证得QB=BC;根据同一平面内垂直于同一直线的两条直线互相平行得出A B ∥ C D ,根据平行于三角形一边的直线截其它两边,所截得的三角形与原三角形相似得出:△QAB∽△QDC;由全等三角形的对应边成比例得出CD=2AB,从而得出答案;
(2)如图2,过点B作BF⊥PC,垂足为F.根据角平分线上的点到角两边的距离相等得出BF=BA=4.根据垂线段最短得出CP≥CD,从而得出CP最小值为8,根据三角形的面积公式进而得出△PBC面积的最小值,进而根据角平分线的定义得出此时△BAP是等腰直角三角形,AP=AB=4,进而得出答案;
(3)此题分两种情况 :①当△BAP∽△CDP时,由∠ B P C = ∠ B P A , ∠ C P D = ∠ B P A 根据平角的定义得出∠BPA=60°,然后利用正切函数的定义得出x=AP=![]() ,②当Δ B A P Δ P D C 时,由∠ C P B = ∠ B P A , ∠ P C D = ∠ B P A ,根据直角三角形两锐角互余得出∠ B P A = 30 ,然后利用正切函数的定义得出x=AP=
,②当Δ B A P Δ P D C 时,由∠ C P B = ∠ B P A , ∠ P C D = ∠ B P A ,根据直角三角形两锐角互余得出∠ B P A = 30 ,然后利用正切函数的定义得出x=AP=![]() ;综上所述从而得出x的值;
;综上所述从而得出x的值;
(4)根据当点A在⊙C上时,由(1)及垂径定理得:AE=AD=DP=![]() x,由全等三角形对应边成比例得出
x,由全等三角形对应边成比例得出


科目:初中数学 来源: 题型:
【题目】如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )

A. 5≤a≤12B. 12≤a≤3![]()
C. 12≤a≤4![]() D. 12≤a≤13
D. 12≤a≤13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( ) 
A.45°
B.54°
C.40°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(m,n+2),B(m+4,n).
(1)当m=2,n=2时,
①如图1,连接AO、BO,求三角形ABO的面积;
②如图2,在y轴上是否存在点P,使三角形PAB的面积等于8,若存在,求P点坐标;若不存在,请说明理由;
(2)如图3,过A、B两点作直线AB,当直线AB过y轴上点Q(0,3)时,试求出m,n的关系式.
(温情提示:(a+b)×(c+d)=ac+ad+bc+bd)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:![]() ;
;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.

求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90°( )
∴EF∥AD( )
∴∠1=∠BAD( )
又∵∠1=∠2(已知)
∴ (等量代换)
∴DG∥BA.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.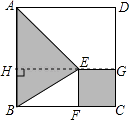
(1)探究1:如果木板边长为1米,FC= ![]() 米,则一块木板用墙纸的费用需元;
米,则一块木板用墙纸的费用需元;
(2)探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,
①用含x的代数式表示y(写过程).
②如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第![]() 回到家中.设小明出发第
回到家中.设小明出发第![]() 时的速度为
时的速度为![]() ,离家的距离为
,离家的距离为![]() ,
,![]() 与
与![]() 之间的函数关系如图所示(图中的空心圈表示不包含这一点).
之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第![]() 时离家的距离为______m;
时离家的距离为______m;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)直接写出![]() 与
与![]() 之间的函数关系式并画出图象.
之间的函数关系式并画出图象.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com