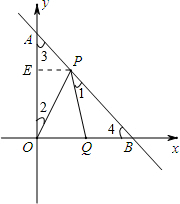
解:(1)由OA=OB=1可知点A、B的坐标是A(0,1),B(1,0),
把A(0,1),B(1,0)代入y=kx+b得:
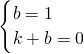
,
解得:k=-1,b=1,
则y=-x+1;
(2)△OPQ可以是等腰三角形.
过P点PE⊥OA交OA于点E,
(ⅰ)若OP=OQ,
则∠OPQ=∠OQP=∠OPQ,
∴∠POQ=90°,
∴点P与点A重合,
∴点P坐标为(0,1),
(ⅱ)若QP=QO,
则∠OPQ=∠QOP=45°,
所以PQ⊥QO,
可设P(x,x)代入y=-x+1得x=

,
∴点P坐标为(

,

),
(ⅲ) 若PO=PQ,
∵∠OPQ+∠1=∠2+∠3,
而∠OPQ=∠3=45°,
∴∠1=∠2,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
PB=OA=1,
∴AP=

-1
由勾股定理求得PE=AE=1-

,
∴EO=

,
∴点P坐标为(1-

,

),
∴点P坐标为(0,1)或(

,

)或(1-

,

)时,△OPQ是等腰三角形.
(3)把x=0代入
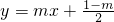
≠1;
把x=

代入
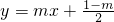
=

;
把x=1-

代入
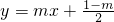
≠

,
所以,(2)中求得的点P,只有当点P坐标为(

,

)时,P点始终在直线
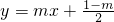
(m≠0)上.
分析:(1)求出A、B点的坐标,利用待定系数法解方程组,求出函数的解析式;
(2)假设存在等腰三角形,分三种情况讨论:(ⅰ)QP=QO;(ⅱ)QP=QO;(ⅲ) 若PO=PQ.能求出P点坐标,则存在点P,否则,不存在.
(3)将(2)中的点代入
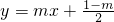
(m≠0),等式成立的点即在直线上.
点评:本题考查了一次函数综合题,属于存在性问题,要分类讨论,同时假设存在,能求出点的坐标,则存在,否则,不存在.

 已知:如图,直线y=kx+b与x轴、y轴分别交于点A、B两点,OA=OB=1,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,射线PQ交x轴于点Q.
已知:如图,直线y=kx+b与x轴、y轴分别交于点A、B两点,OA=OB=1,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,射线PQ交x轴于点Q.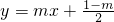 (m≠0)上?请说明理由.
(m≠0)上?请说明理由.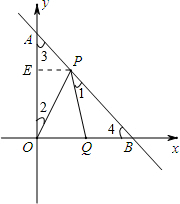 解:(1)由OA=OB=1可知点A、B的坐标是A(0,1),B(1,0),
解:(1)由OA=OB=1可知点A、B的坐标是A(0,1),B(1,0),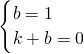 ,
, ,
, ,
, ),
), -1
-1 ,
, ,
, ,
, ),
), ,
, )或(1-
)或(1- ,
, )时,△OPQ是等腰三角形.
)时,△OPQ是等腰三角形.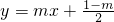 ≠1;
≠1; 代入
代入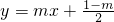 =
= ;
; 代入
代入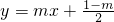 ≠
≠ ,
, ,
, )时,P点始终在直线
)时,P点始终在直线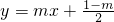 (m≠0)上.
(m≠0)上.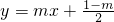 (m≠0),等式成立的点即在直线上.
(m≠0),等式成立的点即在直线上.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=