
【题目】计算:
(1)![]() +(π﹣1)0﹣4
+(π﹣1)0﹣4 ![]() +
+ ![]() (
( ![]() ﹣1)
﹣1)
(2)![]() +
+ ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() )
)
(3)|2 ![]() ﹣3|﹣(﹣
﹣3|﹣(﹣ ![]() )﹣2+
)﹣2+ ![]() .
.
【答案】
(1)解:原式=3 ![]() +1﹣2
+1﹣2 ![]() +
+ ![]() ﹣
﹣ ![]()
= ![]() +
+ ![]()
(2)解:原式=2 ![]() +2
+2 ![]() ﹣
﹣ ![]() +3
+3 ![]()
= ![]() +5
+5 ![]()
(3)解:原式=3﹣2 ![]() ﹣4+3
﹣4+3 ![]()
= ![]() ﹣1
﹣1
【解析】(1)先根据零指数幂的意义计算,再把各二次根式化为最简二次根式,然后合并即可;(2)先把各二次根式化为最简二次根式,然后合并即可;(3)先利用绝对值和负整数指数的意义计算,再把 ![]() 化简,然后合并即可.
化简,然后合并即可.
【考点精析】关于本题考查的零指数幂法则和整数指数幂的运算性质,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能得出正确答案.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C. 
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)如图①,将矩形纸片沿AN折叠,点B落在对角线AC上的点E处,求BN的长;
(2)如图②,点M为AB上一点,将△BCM沿CM翻折至△ECM,ME与AD相交于点G,CE与AD相交于点F,且AG=GE,求BM的长;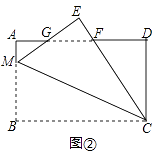
(3)如图③,将矩形纸片ABCD折叠,使顶点B落在AD边上的点E处,折痕所在直线同时经过AB、BC(包括端点),设DE=x,请直接写出x的取值范围: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A. 
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E、F分别是对角线BD上的两点,且BE=DF,连接AE、AF、CE、CF.四边形AECF是什么样的四边形,说明你的道理. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF. 
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com