
分析 (1)根据二次根式的乘法进行计算并化简即可解答本题;
(2)根据式子可知a、b同号,故分两种情况进行计算即可解答本题.
解答 解:(1)$\sqrt{5a}$×2$\sqrt{10b}$
=$2\sqrt{50ab}$
=$10\sqrt{2ab}$;
(2)2b$\sqrt{\frac{a}{b}}$+$\frac{3}{a}$$\sqrt{{a}^{3}b}$-$\sqrt{9ab}$
∵由式子可知,a、b同号,
∴当a>0,b>0时,
原式=$2\sqrt{ab}+3\sqrt{ab}-3\sqrt{ab}$=2$\sqrt{ab}$;
当a<0,b<0时,
原式=$-2\sqrt{ab}-3\sqrt{ab}-3\sqrt{ab}$=$-8\sqrt{ab}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法,注意第(2)小题应分两种情况计算.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
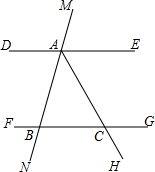 已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.
已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
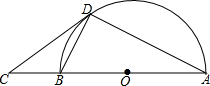 如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.037×1010元 | B. | 2.037×1011元 | C. | 2.037×1012元 | D. | 20.37×1010元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 675×102 | B. | 67.5×102 | C. | 6.75×104 | D. | 6.75×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com