
【题目】如图,直线y1=ax+b与双曲线y2= ![]() 交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).
交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2). 
(1)求直线和双曲线的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
【答案】
(1)解:∵点B(﹣3,﹣2)在双曲线y2= ![]() 上,
上,
∴ ![]() ,
,
∴k=6,
∴双曲线的解析式为y2= ![]() .
.
把y=6代入y2= ![]() 得:x=1,
得:x=1,
∴A的坐标为(1,6),
∵直线y1=ax+b经过A、B两点,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线的解析式为直线y1=2x+4;
(2)解:由直线y1=0得,x=﹣2,
∴点C的坐标为(﹣2,0),
当y1<0时x的取值范围是x<﹣2.
【解析】(1)由点B的坐标求出k=6,得出双曲线的解析式为y2= ![]() .求出A的坐标为(1,6),由点A和B的坐标以及待定系数法即可求出直线的解析式为直线y1=2x+4;(2)求出点C的坐标为(﹣2,0),即可得出当y1<0时x的取值范围.
.求出A的坐标为(1,6),由点A和B的坐标以及待定系数法即可求出直线的解析式为直线y1=2x+4;(2)求出点C的坐标为(﹣2,0),即可得出当y1<0时x的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
(1)小文认为菱形是特殊的“筝形”,你认为他的判断正确吗?
(2)小文根据学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程,请补充完成:
①他首先发现了这类“筝形”有一组对角相等,并进行了证明,请你完成小文的证明过程.
已知:如图,在”筝形”ABCD中,AB=AD,CB=CD.
求证:∠ABC=∠ADC.
证明:②小文由①得到了这类“筝形”角的性质,他进一步探究发现这类“筝形”还具有其它性质,请再写出这类“筝形”的一条性质(除“筝形”的定义外);
③继性质探究后,小文探究了这类“筝形”的判定方法,写出这类“筝形”的一条判定方法(除“筝形”的定义外):
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式x2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B,将直线AB绕着点顺时针旋转90°后,分别与x轴、y轴交于点D、C.
(1)若OB=4,求直线AB的函数关系式;
(2)连接BD,若△ABD的面积是5,求点B的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( ) 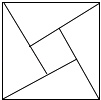
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )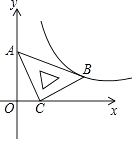
A.( ![]() ,0)
,0)
B.(2,0)
C.( ![]() ,0)
,0)
D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F. 
(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA= ![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度. 
(1)求这个月晴天的天数.
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其它费用,结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( ![]() )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( ![]() )海里.
)海里.
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(参考数据: ![]() =1.41,
=1.41, ![]() =1.73,
=1.73, ![]() =2.45)
=2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com