
【题目】如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
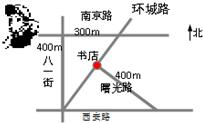
A、600mB、500m
C、400mD、300m
【答案】B
【解析】由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
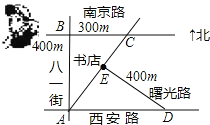
解:如右图所示,
∵BC∥AD,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=![]() =500m,
=500m,
∴CE=AC-AE=200,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故选B.
本题考查了平行线的性质、全等三角形的判定和性质、勾股定理.解题的关键是证明△ABC≌△DEA,并能比较从B到E有两种走法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) 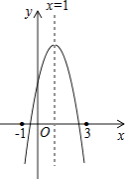
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.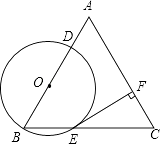
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.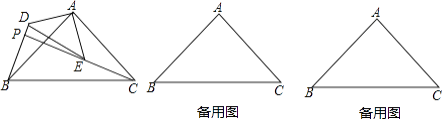
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( ) 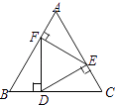
A.1:3
B.2:3
C.![]() :2
:2
D.![]() :3
:3
查看答案和解析>>
科目:初中数学 来源: 题型:
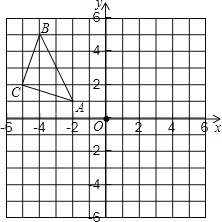
【题目】操作探究:如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(–2,1),B(–4,5),C(–5,2).
(1)作△ABC关于直线l:x=–1对称的△A1B1C1,其中,点A, B,C的对称点分别为点A1,B1,C1;
(2)写出点C1的坐标__________;
(3)在平面直角坐标系中有一点P位于第四象限,其坐标表示为P(m,n),则点P关于直线l的对称点Q的坐标表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.

(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com