
 已知等腰梯形ABCD,AD∥BC,AD=4,∠B=60°,AC为∠DCB的平分线,E是AB的中点,DF是梯形的高,SABCD=________;若在直线AC上找一点M,使EM+FM的值最小,则其最小值=________.
已知等腰梯形ABCD,AD∥BC,AD=4,∠B=60°,AC为∠DCB的平分线,E是AB的中点,DF是梯形的高,SABCD=________;若在直线AC上找一点M,使EM+FM的值最小,则其最小值=________. 6
6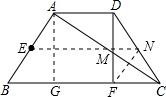 解:过点A作AG⊥BC于G,
解:过点A作AG⊥BC于G, ,
, ×(4+8)×2
×(4+8)×2 =12
=12 ;
; ×(4+8)=6.
×(4+8)=6. ;6.
;6.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com