练习册

  • 练习册
  • 试题
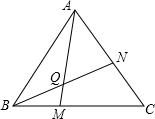
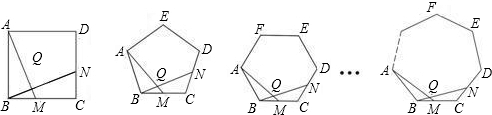
    精英家教网 > 初中数学 > 题目详情

    如图，正△ABC，将此三角形绕点C顺时针旋转，使CB与CA重合，得△ACD．
    （1）作出△ACD；
    （2）四边形ABCD是什么四边形？

    解：（1）如图所示：

    （2）∵△ACD是△ABC旋转所得，
    ∴△ACD≌△BCA，
    ∴∠DAC=∠BCA，∠BAC=∠ACD，
    ∴AD∥BC，AB∥CD，
    ∴四边形ABCD是平行四边形，
    又∵AD=AB，
    ∴四边形ABCD是菱形．
    分析：（1）作图，按题中给出的条件画出图形，且使CB与CA重合．
    （2）两个全等三角形，四条边相等，且对边平行，所以可推出其为菱形．
    点评：熟练掌握菱形的性质及判定定理，并熟悉正三角形的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （1）如图，正△ABC中，点M与点N分别是BC、CA上的点，且BM=CN，连接AM、BN，两线交于点Q，求∠AQN的度数．
    精英家教网
    （2）将1题中的“正△ABC”分别改为正方形ABCD，正五边形ABCDE，正六边形ABCDEF，…，正n边形ABCD…N，其余条件不变，根据第1题的求解思路分别推断∠AQN的度数，将结论填入下表：
    正多边形 正方形 正五边形 正六边形 … 正n边形
    ∠AQN的度数
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    19、如图，正△ABC，将此三角形绕点C顺时针旋转，使CB与CA重合，得△ACD．
    （1）作出△ACD；
    （2）四边形ABCD是什么四边形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，正△ABC的边长为3，绕其中心O将△ABC旋转180°得到△DEF，则△ABC和△DEF重叠部分的面积为（　　）
    A、
    3
    		3
    2
    B、
    3
    		3
    4
    C、
    		3
    2
    D、6
    		3

    查看答案和解析>>

    科目：初中数学 来源：2012届浙江省温州市四校联盟九年级下学期一模数学试卷（带解析） 题型：填空题

    如图，正△ABC的边长为4，⊙O与正△ABC的边AB，BC都相切，点D，E，F分别在边AC，AB，BC上，现将正△ABC沿着DE，DF折叠，点A，点C都恰好落在圆心O处，连接EF，若EF恰好与⊙O相切，则⊙O的半径为__    _．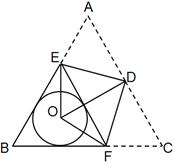

    查看答案和解析>>

    同步练习册答案