
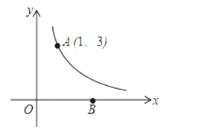
【题目】如图,反比例函数y=![]() (k为常数,且k≠5)经过点A(1,3).
(k为常数,且k≠5)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】明明利用自制“四旋翼”无人机进行数学研究活动,无人机传递数据显示,无人机A与地面CD的距离为420米,从无人机底部A处看“河南大玉米”(郑州会展中心千禧大夏)顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,求“河南大玉米”的高度.(![]() ,
,![]() ,
,![]() ≈2.236,结果精确到1m.)
≈2.236,结果精确到1m.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.
的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.

查看答案和解析>>
科目:初中数学 来源: 题型:
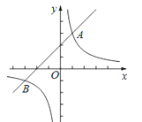
【题目】如图,一次函数y=x+2的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
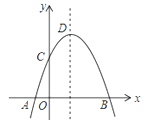
A. ① B. ② C. ③ D. ①②③都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
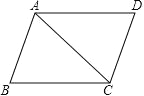
【题目】如图,四边形ABCD 是平行四边形,AB=c,AC=b,BC=a,抛物线 y=ax2+bx﹣c 与 x 轴的一个交点为(m,0).
(1)若四边形ABCD是正方形,求抛物线y=ax2+bx﹣c的对称轴;
(2)若 m=![]() c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com