解答:解:(1)设所求抛物线的解析式为:y=a(x-1)
2+4,
将点B(3,0)代入,得:a(3-1)
2+4=0
解得:a=-1,
∴解析式为:y=-(x-1)
2+4;
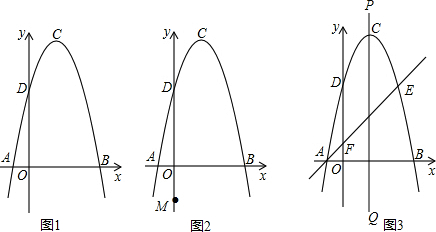
(2)如图2,当MN∥AB时,
∵0=-(x-1)
2+4;
∴x
1=-1,x
2=3,
∴AB=4,
∵M(0,-1),
∴-1=-(x-1)
2+4,
解得:x
1=1+
,x
2=1-
,
∴MN=
-1≠AB,MN′=1+
≠AB,
∴此时四边形ANMB是梯形,四边形AMN′B是梯形,N(1-
,-1),N′(-1-
,-1),
当AM∥BN″时,
∵A(-1,0),M(0,-1),设直线AM的解析式为y=kx+b,

则
,
解得:
,
∴直线AM的解析式为y=-x-1,
∴BN″的解析式为:y=-x+d,
将B(3,0)代入得出:0=-3+d,
解得:d=3,
∴BN″的解析式为:y=-x+3,
∴联立两函数得:
,
解得:
,
,
∴N″的坐标为:(0,3),此时AM≠BN″,
∴四边形AMBN″是梯形,
∴综上所述:以B、A、M、N为顶点的四边形是梯形,
则点N的坐标为:(0,3),(1-
,-1),(-1-
,-1);
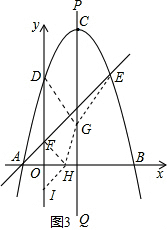
(3)如图3,在y轴的负半轴上取一点I,使得点F与点I关于x轴对称,
在x轴上取一点H,连接HF、HI、HG、GD、GE,则HF=HI,点E坐标为(2,3)
∴点A(-1,0),点B(3,0),点D(0,3)
又∵抛物线的对称轴为:直线x=1.
∴点D与点E关于PQ对称,GD=GE 过A、E两点的一次函数解析式为:y=x+1
∴当x=0时,y=1
∴点F坐标为(0,1)
∴DF=2
又∵点F与点I关于x轴对称,∴点I坐标为(0,-1)
∴EI=
=
=2
,
又∵要使四边形DFHG的周长最小,由于DF是一个定值,
∴只要使DG+GH+HI最小即可 DG+GH+HF=EG+GH+HI
只有当EI为一条直线时,EG+GH+HI最小,过E(2,3)、I(0,-1)
解析式为:y=2x-1
∴当x=1时,y=1;当y=0时,x=
;
∴点G坐标为(1,1),点H坐标为(
,0)
∴四边形DFHG的周长最小为:DF+DG+GH+HF=DF+EI=2+2
.





 阅读快车系列答案
阅读快车系列答案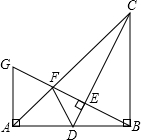 如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论:①
如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论:①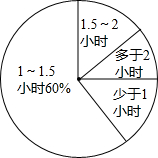 为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
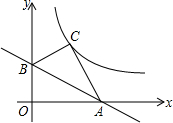 如图,点A(3,0),B(0,
如图,点A(3,0),B(0,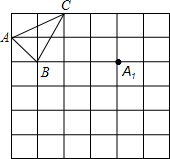 作图题:如图是6×6的网格,已知格点△ABC和格点A1.
作图题:如图是6×6的网格,已知格点△ABC和格点A1.