
【题目】 (10分)已知抛物线![]() 与
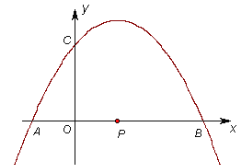
与![]() 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
(1)直接写出抛物线的对称轴,及抛物线与![]() 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点![]() ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】见解析
【解析】
(1)根据对称轴公式,对称轴x=﹣![]() =1;
=1;
点B的坐标是(3,0).(2分)
(2)点C在以AB为直径的⊙P上,∴∠ACB=90°
由∠ACB=∠AOC=∠COB=90°得△AOC∽△COB,
∴![]() ,
,
∴CO=![]() ,
,
∴b=![]()
当x=﹣1,y=0时,﹣a﹣2a+![]() =0,
=0,
∴a=![]() ,
,
∴y=﹣![]() ;(6分)
;(6分)
(3)点M的坐标有三种情况,如果以AB为平行四边形的对角线,那么P(1,0)就是平行四边开的对称中心,即C点与M点关于P点位对称,设M点坐标为(x,y).
那么![]() ,x=2 .
,x=2 . ![]() ,y=
,y=![]() .∴M点坐标为(2,
.∴M点坐标为(2,![]() )
)
同理以AC、BC为对称轴得出M点的坐标为(-4,![]() )、(4,
)、(4,![]() )
)
分别是:(2,![]() ),(-4,
),(-4,![]() )或(4,
)或(4,![]() ).(10分)
).(10分)



科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球个数是白球的3倍多10个.已知从袋中摸出一个球是红球的概率是 ![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走5个球(其中没有红球)求从剩余球中摸出球是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验的总次数、频数及频率三者的关系是( )
A. 频数越大,频率越大
B. 频数与总次数成正比
C. 总次数一定时,频数越大,频率可达到很大
D. 频数一定时,频率与总次数成反比
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了响应国家阳光体育活动,选派部分学生参加足球、乒乓球、篮球、排球队集训.根据参加项目制成如下两幅不完整的统计图(要求每位同学只能选择一种自己喜欢的球类,图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数,请你根据图中提供的信息解答下列问题:
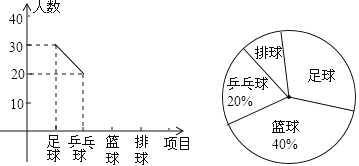
(1)参加篮球队的有 人,参加足球队的人数占全部参加人数的 %.
(2)喜欢排球队的人数在扇形统计图中所占的圆心角是多少度?并补全频数分布折线统计图.
(3)若足球队只剩一个集训名额,学生小明和小虎都想参加足球队,决定采用随机摸球的方式确定参加权,具体规则如下:一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球,小明随机地从四个小球中摸出一球然后放回,小虎再随机地摸出一球,若小明摸出的小球标有数字比小虎摸出的小球标有的数字大,则小明参加;若小明摸出的小球标有数字比小虎摸出的小球标有的数字小,则小虎参加,试分析这种规则对双方是否公平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com