
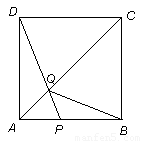
如图,在边长为4的正方形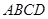 中,点
中,点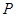 在
在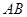 上从
上从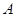 向
向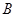 运动,连接
运动,连接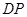 交
交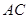
于点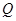 .
.
⑴试证明:无论点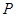 运动到
运动到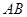 上何处时,都有△
上何处时,都有△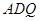 ≌△
≌△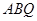 ;
;
⑵当点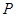 在
在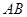 上运动到什么位置时,△
上运动到什么位置时,△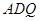 的面积是正方形
的面积是正方形 面积的
面积的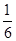 ;
;
⑶若点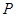 从点
从点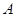 运动到点
运动到点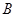 ,再继续在
,再继续在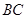 上运动到点
上运动到点 ,在整个运动过程中,当点
,在整个运动过程中,当点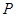 运动到什么位置时,△
运动到什么位置时,△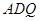 恰为等腰三角形.
恰为等腰三角形.
⑴证明:在正方形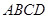 中,无论点
中,无论点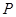 运动到
运动到 上何处时,都有
上何处时,都有
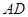 =
= ∠
∠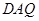 =∠
=∠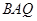
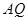 =
=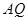 ∴△
∴△ ≌△
≌△
⑵△ 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的 时,
时,
过点Q作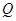
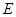 ⊥
⊥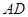 于
于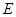 ,
,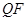 ⊥
⊥ 于
于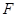 ,
,

则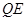 =
= 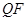
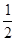
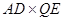 =
= =
=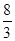 ∴
∴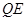 =
=
由△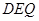 ∽△
∽△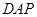 得
得 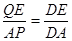 解得
解得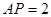
∴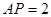 时,△
时,△ 的面积是正方形
的面积是正方形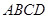 面积的
面积的
⑶若△ 是等腰三角形,则有
是等腰三角形,则有
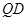 =
=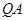 或
或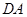 =
=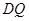 或
或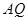 =
=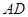
①当点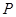 运动到与点
运动到与点 重合时,由四边形
重合时,由四边形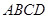 是正方形知
是正方形知 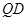 =
=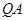
此时△ 是等腰三角形
是等腰三角形
②当点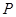 与点
与点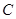 重合时,点
重合时,点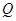 与点
与点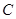 也重合,此时
也重合,此时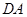 =
=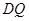 , △
, △ 是等腰三角形
是等腰三角形
③:如图,
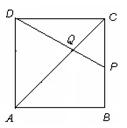
设点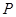 在
在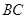 边上运动到
边上运动到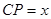 时,有
时,有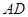 =
=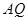
∵ 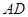 ∥
∥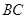 ∴∠
∴∠ =∠
=∠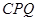
又∵∠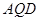 =∠
=∠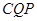 ∠
∠ =∠
=∠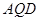
∴∠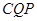 =∠
=∠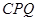 ∴
∴ 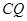 =
= =
=
∵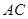 =
=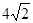
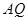 =
=
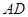 =4
∴
=4
∴
即当 时,△
时,△ 是等腰三角形.
是等腰三角形.
【解析】(1)两边一角 AQ=AQ ,AB=AD=4,∠DAQ=∠BAQ=45度 所以两个三角形全等。
(2)做QE垂直于AD, △DQE相似于△DPA ,△ADQ面积=AD QE/2,正方形面积=AD
QE/2,正方形面积=AD AB,△ ADQ的面积是正方形面积的1/6, 则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3, △DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4= 4/3 /AP,故AP=2,因为AB=4 则P点正好运动到AB的中点
AB,△ ADQ的面积是正方形面积的1/6, 则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3, △DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4= 4/3 /AP,故AP=2,因为AB=4 则P点正好运动到AB的中点
(3)假设△ADQ恰好为等腰三角形::P在 ABC上运动 首先当AD=QD=4时 Q与C点刚好重合 所以P运动到C点 △ADQ为等腰三角形;当P运动到B点时,AQ=QD △ADQ为等腰直角三角形;当AD=AQ=4时,△ADQ与△CPQ相似,则PC=CQ=AC-AQ=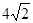 -4,则P运动到距离C点
-4,则P运动到距离C点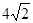 -4时,△ADQ为等腰三角形
-4时,△ADQ为等腰三角形


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
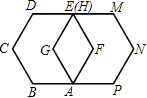 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )查看答案和解析>>
科目:初中数学 来源:初三数学圆及旋转题库 第8讲:弧长和扇形面积(解析版) 题型:解答题
 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com