
【题目】若等腰三角形一腰上的中线分周长为6cm或9cm两部分,求这个等腰三角形的底边和腰的长.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】对x,y定义了一种新运算T,规定T(x,y)= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= ![]() ,已知T(1,﹣1)=﹣2,T(4,2)=1.
,已知T(1,﹣1)=﹣2,T(4,2)=1.
(1)求a,b的值;
(2)若关于m的不等式组 ![]() 恰好有3个整数解,求p的取值范围.
恰好有3个整数解,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A2处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015,到BC的距离记为h2015.若h1=1,则h2015的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( ) 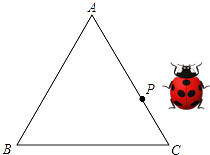
A.d>h
B.d<h
C.d=h
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司今年元月份利润为500万元,以后两个月均匀增长,第一季度的利润1820万元,设该公司利润月平均增长率为x,根据题意可列方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
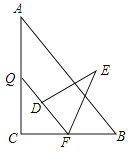
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com