

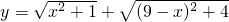 ,当x为何值时,y的值最小,并求出这个最小值.
,当x为何值时,y的值最小,并求出这个最小值.

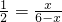 ,
,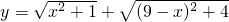 中的
中的  即是图中的AP,
即是图中的AP,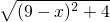 即是图中的BP.
即是图中的BP.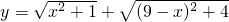 的最小值就是AP+BP的最小值,
的最小值就是AP+BP的最小值, ,
, ,
,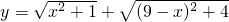 有最小值,
有最小值, .
.
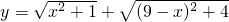 中即可求出其最小值.
中即可求出其最小值.

科目:初中数学 来源: 题型:
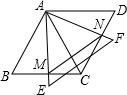 绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 20、在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图),把余下的部分拼成一个矩形(如图),根据两个图形中阴影部分的面积相等,可以验证的乘法公式是
20、在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图),把余下的部分拼成一个矩形(如图),根据两个图形中阴影部分的面积相等,可以验证的乘法公式是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知两个两条直角边长分别为a,b的直角三角形纸片和一个两条直角边长都为c的直角三角形纸片,用这三个直角三角形纸片恰好拼成一个梯形.请用两种方法计算梯形的面积(含有a、b、c的代数式表示).
如图,已知两个两条直角边长分别为a,b的直角三角形纸片和一个两条直角边长都为c的直角三角形纸片,用这三个直角三角形纸片恰好拼成一个梯形.请用两种方法计算梯形的面积(含有a、b、c的代数式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com