
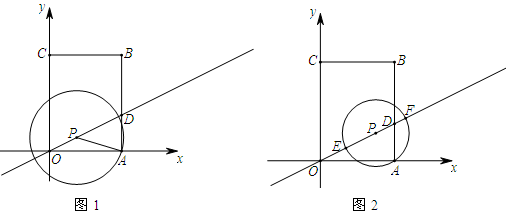
���� ��1���ɡ�OPC�ס�ADP���ɵ�$\frac{AP}{PC}=\frac{AD}{OC}$�����AC��AD���ɽ�����⣻
��2��ֻҪ֤����PDA=��DAP���ɣ�
��3���ٷ��������ηֱ���⼴�ɢ�����ͼ2�У�����M��OC�е㣬PM=PA��������ͼ3�У�����M��OA�е㣬PM=PA��������ͼ4�У�����M��AB�е㣬PM=PA��������ͼ5�У�����M��BC�е㣬PM=PA��
����ͼ6�У���DE=3DFʱ����֪PA=2PD���ɴ��г����̼��ɽ�����⣮
��� �⣺��1����ͼ1�У�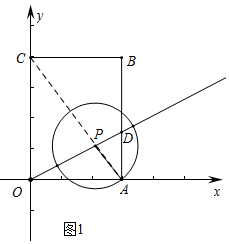
��B��3��4����BC=3��AB=4
�ߡ�B=90���AC=5
��OC��AB��
���OPC�ס�ADP��
��$\frac{AP}{PC}=\frac{AD}{OC}$��
��$\frac{AP}{5-AP}=\frac{1.5}{4}$
��$AP=\frac{15}{11}$��
��2���ߡ�P������O��
��OP=AP
���POA=��PAO��
�ߡ�PDA+��POA=��DAP+��PAO��
���PDA=��DAP��
���PAD�ǵ��������Σ�
��3���ٷ�4���������ۣ�
������ͼ2�У�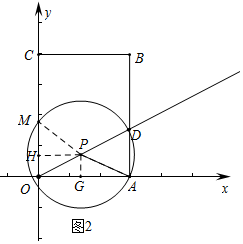
����M��OC�е㣬PM=PA
��${m^2}+{��2-\frac{1}{2}m��^2}={��\frac{1}{2}m��^2}+{��3-m��^2}$��
���$m=\frac{5}{4}$��
������ͼ3�У�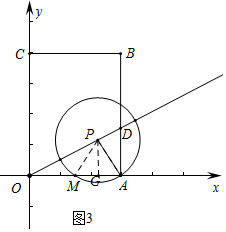
����M��OA�е㣬PM=PA
��MG=GA=$\frac{3}{4}$��
��$m=\frac{3}{2}+\frac{3}{4}=\frac{9}{4}$��
������ͼ4�У�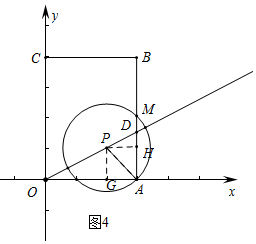
����M��AB�е㣬PM=PA
��PG=$\frac{1}{2}$AM=1��
��PH=2DH=2��$��\frac{3}{2}-1��$=1��
��m=2��
������ͼ5�У�
����M��BC�е㣬PM=PA
��${��m-\frac{3}{2}��^2}+{��\frac{1}{2}m-4��^2}={��m-3��^2}+{��\frac{1}{2}m��^2}$��
���$m=\frac{37}{4}$��
��������������Ҫ���mֵΪ$\frac{5}{4}$��$\frac{9}{4}$��2��$\frac{37}{4}$��
����ͼ6�У���DE=3DFʱ����֪PA=2PD��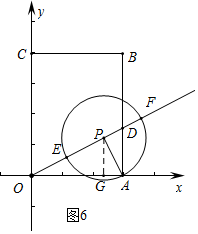
��P��m��$\frac{m}{2}$������$\sqrt{��m-3��^{2}+��\frac{m}{2}��^{2}}$=2$\sqrt{��m-3��^{2}+��\frac{m}{2}-\frac{3}{2}��^{2}}$��
���m=$\frac{12}{5}$��4��
��m=4ʱ��ED=$\frac{1}{3}$DF��
���Ͽ�֪����DE��DF����$\frac{1}{3}$��$\frac{DE}{DF}$��3ʱ��m��ȡֵ��ΧΪ$\frac{12}{5}$��m��4��
���� ���⿼��Բ�ۺ��⡢���������ε��ж������ʡ����ε����ʡ����ɶ������������빫ʽ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ѧ��ؼ����̣�������ת��Ϊ���̽���������п�ѹ���⣮


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | 60��x��90 | 90��x��120 | 120��x��150 | 150��x��180 | 180��x��210 |
| Ƶ�� | 16 | 25 | 9 | 7 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���AOB���������������ֱ���A��6��6����O��0��0����B��8��0������M��OB��������O��B��һ���㣬MN��AB��OA�ڵ�N����P��AB��������㣬����AM��PM��PN��BN�����M�������ǣ�t��0������PMN�����ΪS��
��ͼ����ƽ��ֱ������ϵ�У���AOB���������������ֱ���A��6��6����O��0��0����B��8��0������M��OB��������O��B��һ���㣬MN��AB��OA�ڵ�N����P��AB��������㣬����AM��PM��PN��BN�����M�������ǣ�t��0������PMN�����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
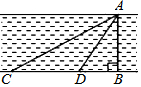 ��ͼ�������ӿ�AB������ӵ�����ƽ�У�����C���á�ACB=30�㣬D���á�ADB=60�㣬��CD=100m����ӿ�ABΪ50$\sqrt{3}$m������������ţ���
��ͼ�������ӿ�AB������ӵ�����ƽ�У�����C���á�ACB=30�㣬D���á�ADB=60�㣬��CD=100m����ӿ�ABΪ50$\sqrt{3}$m������������ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����5��5�������������У�ÿ��С�����εı߳�����1����λ���ȣ��߶�AB�Ķ����ڸ�㣨С�����εĶ��㣩�ϣ�
��ͼ����5��5�������������У�ÿ��С�����εı߳�����1����λ���ȣ��߶�AB�Ķ����ڸ�㣨С�����εĶ��㣩�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
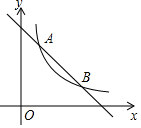 ��ͼ��һ�κ���y=-x+3��ͼ���뷴����y=$\frac{k}{x}$��kΪ��������k��0����ͼ����A��1��a����B���㣮
��ͼ��һ�κ���y=-x+3��ͼ���뷴����y=$\frac{k}{x}$��kΪ��������k��0����ͼ����A��1��a����B���㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com