
 如图所示,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,连接CD交OE于F,则下列结论不能够由上述条件证得的是( )
如图所示,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,连接CD交OE于F,则下列结论不能够由上述条件证得的是( )
|


科目:初中数学 来源: 题型:
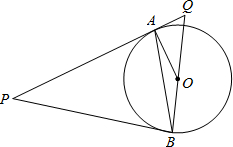 =PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.| 4 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,直线是四边形ABCD的对称轴,若AB=CD,则下列结论:
如图所示,直线是四边形ABCD的对称轴,若AB=CD,则下列结论:查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(贵州黔南州卷)数学 题型:解答题
如图所示,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O 上一点,且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
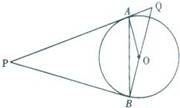 (1)求证:PB是⊙O的切线;
(1)求证:PB是⊙O的切线;
(2)求证:AQ•PQ=OQ•BQ;
(3)设∠AOQ=α,若cosα= ,OQ=15,求AB的长.
,OQ=15,求AB的长.
[来源:ZXXK]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com