
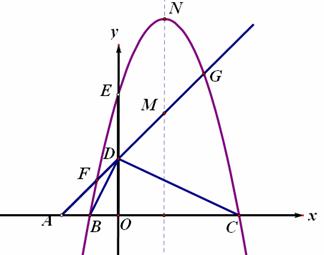
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q。
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断⊿BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物 线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由。
线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由。
(1)B(-1,0) E(0,4) C(4,0) 设 解析式是
解析式是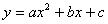
可得 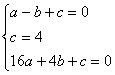 解得
解得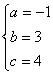 (2分) ∴
(2分) ∴ (1分)
(1分)
(2)⊿BDC是直角三角形 (1分)
∵BD2=BO2+DO2=5 , DC2=DO2+CO2=20 ,BC2=(BO+CO)2=25
∴BD2+ DC2= BC2  (1分)
(1分)
∴⊿BDC是Rt⊿
点A坐标是(-2,0),点D坐标是(0,2)直线AD的解析式是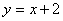 (1分)
(1分)
设点P坐标是(x,x+2)
当OP=OC时 x2+(x+2)2=16 解得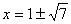 (
(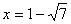 不符合,舍去)此时点P(
不符合,舍去)此时点P(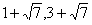 )
)
当PC=OC时 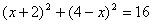 方程无解
方程无解
当PO=PC时,点P在OC的中垂线上,∴点P横坐标是2, 得点P坐标是(2,4)
∴当⊿POC是等腰三角形时,点P坐标是(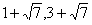 )或(2,4) (2分)
)或(2,4) (2分)
(3) 点M坐标是(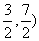 )N坐标是(
)N坐标是(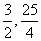 )∴MN=
)∴MN=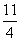
设点P 为(x,x+2)Q(x,-x2+3x+4),则PQ=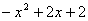
①若PQNM是菱形,则PQ=MN,可得x1=0.5 x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=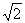 ,所以菱形不存在(2分)
,所以菱形不存在(2分)
②能成为等腰梯形,此时点P的坐标是(2.5,4.5)(2分)


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
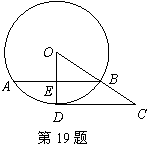
如图, CD切⊙O于点D,连结OC, 交⊙O于点B,过点B作弦 AB⊥OD,点E为垂足,已知⊙O的半径为10,sin∠COD=
AB⊥OD,点E为垂足,已知⊙O的半径为10,sin∠COD=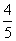 .
.
求:(1)弦AB的长;
(2)CD的长;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
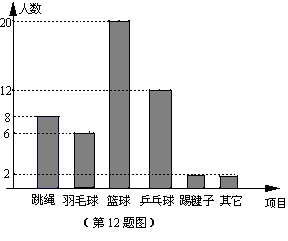
“阳光体育”活动在滨江学校轰轰烈烈第开展,为了解同学们最喜爱的体育运动项目,小李对本班50名同学进行了跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目最喜爱人数的调查,并根据调查结果绘制了如下的人数分布直方图,若将其转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为 .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某班第二组女生参加体育测试,仰卧起坐的成绩(单位:个)如下:
43、41、39、40、37.这组数据的中位数是___________;标准差是_______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com