Question

【题目】如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．

（1）判断直线DE与⊙O的位置关系，并说明理由；

（2）若AC=6，BC=8，OA=2，求线段DE的长．

Answer 1

【答案】（1）直线DE与⊙O相切；（2）4.75．

【解析】试题分析：(1) 直线DE与⊙O相切，连接OD，根据等腰三角形的性质可得∠A=∠ODA，根据线段垂直平分线的性质及等腰三角形的性质易得∠B=∠EDB，易证ODA＋∠EDB＝，即可得∠ODE＝－＝，所以直线DE与⊙O相切；（2）连接OE，设DE=x，则EB=ED=x，CE=8-x.因∠C=∠ODE =，根据勾股定理可得，即，解得x的值即可得线段DE的长.

试题解析： (1) 直线DE与⊙O相切.

理由如下：

连接OD，

∵OD=OA，

∴∠A=∠ODA.

∵EF是BD的垂直平分线，

∴EB="ED."

∴∠B=∠EDB.

∵∠C=，

∴∠A＋∠B＝.

∴∠ODA＋∠EDB＝.

∴∠ODE＝－＝.

∴直线DE与⊙O相切.

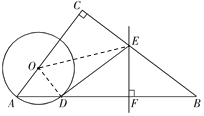
(2) 解法一：

连接OE，

设DE=x，则EB=ED=x，CE=8-x.

∵∠C=∠ODE =，

∴.

∴.

∴.

即DE=.

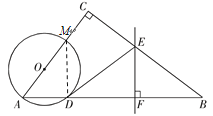
解法二：

连接DM，

∵AM是直径，

∴∠MDA＝，AM=4.

又∵∠C=，

∴,

.

∴, ∴AD=2.4.

∴BD=10-2.4=7.6.

∴BF=.

∵EF⊥BD，∠C=，

∴.

∴, BE=.

∴DE=.