
 如图,两个正方形ABDE和ACFG如图摆放.
如图,两个正方形ABDE和ACFG如图摆放.分析 (1)结论:BM⊥CM.如图1中,延长BM到H,使得MH=BM,连接BF、DH、AF、EH、CE、BC、BC、CH.首先证明四边形BDFH,四边形AEHF是平行四边形,再证明△BAC≌△HFC,利用等腰直角三角形的性质即可解决问题.
(2)过G作GT∥AE交AH的延长线于T.连接ET.由△GAT≌△ADB,推出GT=AB=AE,由GT∥AE,推出四边形AGTE是平行四边形,即可解决问题.
(3)过A作AS⊥BC于Q,且AS=BC,连接PS、CS、BS.先证明△BCF≌△SAC,△BAS≌△DBC,想办法证明S是△BCP的垂心,推出A、S、P共线,即可解决问题.
解答 (1)解:结论:BM⊥CM.
理由:延长BM到H,使得MH=BM,连接BF、DH、AF、EH、CE、BC、BC、CH.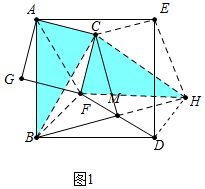
∵四边形ABDE、四边形AGFC是正方形,
∴AC=FC,AB=BD,∠CAF=∠CFA=45°,∠GAC=∠BAE=90°,
∴∠BAG=∠EAC,
∵BM=MH,FM=DM,
∴四边形BDHF是平行四边形,
∴BD∥FH∥AE,BD=FH=AE,
∴四边形AFHE是平行四边形,
∴∠CFH+∠CFA+∠FAC+∠EAC=180°,
∴∠CFH=90°-∠EAC=90°-∠BAG=∠BAC,
在△BAC和△HFC中,
$\left\{\begin{array}{l}{AC=CF}\\{∠BAC=∠CFH}\\{AB=FH}\end{array}\right.$,
∴△BAC≌△HFC,
∴BC=CH,∠ACB=∠FCH,
∴∠BCH=∠ACF=90°,
∵BM=MH,
∴CM⊥BH,CM=BM=MH,
∴CM⊥BM,CM=BM.
(2)证明:过G作GT∥AE交AH的延长线于T.连接ET.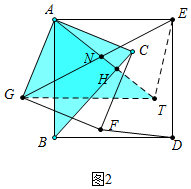
∵AT⊥BC,
∴∠AHC=∠AHB=∠GAC=90°,
∴∠GAT+∠CAH=90°,∠CAH+∠ACH=90°,
∴∠GAT=∠ACB,
∵∠ABC+∠BAH=90°,∠BAH+∠ATG=90°,
∴∠ABC=∠ATG,
∵AG=AC,
∴△GAT≌△ADB,
∴GT=AB=AE,∵GT∥AE,
∴四边形AGTE是平行四边形,
∴GN=NE.
(3)证明:过A作AS⊥BC于Q,且AS=BC,连接PS、CS、BS.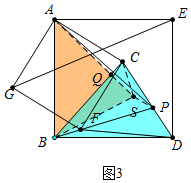
∵∠CAS+∠ACQ=90°,∠ACQ+∠BCF=90°,
∴∠CAS=∠BCF,∵AC=CF,AS=BC,
∴△BCF≌△SAC,
∴∠FBC=∠CSA,
∵∠CSA+∠SCQ=90°,
∴∠SCQ+∠FBC=90°,
∴CS⊥BP,
∵∠ABQ+∠BAS=90°,∠ABQ+∠DBC=90°,
∴∠BAS=∠DBC,
∵AB=BD,BC=AS,
∴△BAS≌△DBC,
∴∠BCD=∠ASB,
∵∠ASB+∠SBQ=90°,
∴∠BCD+∠SBQ=90°,
∴BS⊥CD,∵CS⊥BP,
∴S是△BCP的垂心,
∴PS⊥BC,∵SA⊥BC,
∴A、S、P共线,
∴AP⊥BC.
点评 本题考查四边形综合题、全等三角形的判定和性质、正方形的性质、旋转变换、平行四边形的判定和性质、垂心等知识,解题的关键是学会添加辅助线构造全等三角形解决问题,第三个问题比较难,证明S是△BCP的垂心是突破口,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
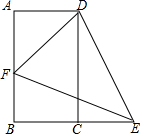 已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.
已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
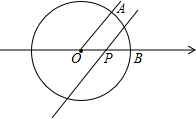 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若点P对应的实数为x,过点P且与OA平行的直线与⊙O没有公共点,则x的取值范围是-$\sqrt{2}$≤x≤$\sqrt{2}$且x≠0.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若点P对应的实数为x,过点P且与OA平行的直线与⊙O没有公共点,则x的取值范围是-$\sqrt{2}$≤x≤$\sqrt{2}$且x≠0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com