
分析 (1)根据题意可以判断题目中的式子哪些是真分式,哪些是假分式;
(2)根据题意可以将题目中的式子写出整式与真分式的和的形式;
(3)根据题意可以将题目中的式子化简变为整式与真分式的和的形式.
解答 解:(1)根据题意可得,
$\frac{a-2}{a+1}$、$\frac{{x}^{2}}{x+1}$、$\frac{{a}^{2}+3}{{a}^{2}-1}$都是假分式,$\frac{2b}{{b}^{2}+3}$是真分式,
故答案为:③;
(2)由题意可得,
$\frac{4a+3}{2a-1}$=$\frac{4a-2+5}{2a-1}=2+\frac{5}{2a-1}$,
若假分式$\frac{4a+3}{2a-1}$的值为正整数,
则$\frac{5}{2a-1}=-1$或2a-1=1或2a-1=5,
解得,a=-2或a=1或a=3,
故答案为:2、$\frac{5}{2a-1}$,-2、1或3;
(3)$\frac{{a}^{2}+3}{a-1}$=$\frac{{a}^{2}-1+4}{a-1}=\frac{{a}^{2}-1}{a-1}+\frac{4}{a-1}=a+1+\frac{4}{a-1}$,
故答案为:a+1+$\frac{4}{a-1}$.
点评 本题考查分式的混合运算,解答本题的关键是明确题意,利用题目中的新规定解答问题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
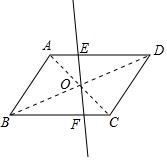 观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?
观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 足球比赛胜5场与负6场 | B. | 向东走3千米,再向前走3千米 | ||
| C. | 增产10吨粮食与减产-10吨粮食 | D. | 下降的反义词是上升 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com