
 AC,同理可得IG∥BD,IG=
AC,同理可得IG∥BD,IG= BD,易求AC=BD,又由于GF∥AC,∠IGF=90°,利用平行线性质可得∠IHO=90°,而IG∥BD,易证∠BOC=90°,即AC⊥BD,从而可证四边形ABCD的对角线互相垂直且相等.
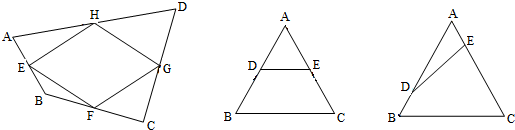
BD,易求AC=BD,又由于GF∥AC,∠IGF=90°,利用平行线性质可得∠IHO=90°,而IG∥BD,易证∠BOC=90°,即AC⊥BD,从而可证四边形ABCD的对角线互相垂直且相等. 解:如右图所示,四边形ABCD的各边中点分别是I、E、F、G,且四边形EFGI是正方形,
解:如右图所示,四边形ABCD的各边中点分别是I、E、F、G,且四边形EFGI是正方形, AC,
AC, BD,
BD, AC=
AC= BD,
BD,

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在边长为1的正方形网格中,△A′B′C′与△ABC是中心对称图形.
如图,在边长为1的正方形网格中,△A′B′C′与△ABC是中心对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2008年内蒙古鄂尔多斯市东胜实验中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com