
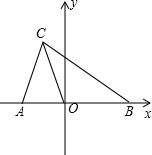
 ��ͼ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C��-1��3������|$\frac{a}{2}$$+\frac{b}{3}$|+��4a-b+11��2=0��
��ͼ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C��-1��3������|$\frac{a}{2}$$+\frac{b}{3}$|+��4a-b+11��2=0������ ��1������|$\frac{a}{2}$$+\frac{b}{3}$|+��4a-b+11��2=0���ɵ�$\left\{\begin{array}{l}{\frac{a}{2}+\frac{b}{3}=0}\\{4a-b+11=0}\end{array}\right.$���ݴ����a��b��ֵ���ɣ�
��2�����ȹ���C��CG��x�ᣬCH��y�ᣬ����ֱ�ΪG��H��Ȼ����������ε�������������ABC�����������������2�������COM������Ƕ��٣����������M�����꼴�ɣ�
��3�����ȸ��ݵ�M�������ǣ�0��-7.5��ʱ����COM�����=$\frac{1}{2}$��ABC��������ɵõ�M�������ǣ�0��7.5��ʱ����COM�����=$\frac{1}{2}$��ABC�������Ȼ����������εĸ�һ��ʱ������͵׳����ȣ��ɵõ�M�������ǣ�2.5��0����-2.5��0��ʱ����COM�����=$\frac{1}{2}$��ABC��������ݴ˽�ɣ�
���  �⣺��1����|$\frac{a}{2}$$+\frac{b}{3}$|+��4a-b+11��2=0��
�⣺��1����|$\frac{a}{2}$$+\frac{b}{3}$|+��4a-b+11��2=0��
��$\left\{\begin{array}{l}{\frac{a}{2}+\frac{b}{3}=0}\\{4a-b+11=0}\end{array}\right.$
���$\left\{\begin{array}{l}{a=-2}\\{b=3}\end{array}\right.$
��a��ֵ��-2��b��ֵ��3��
��2����ͼ1������C��CG��x�ᣬCH��y�ᣬ����ֱ�ΪG��H��
��A��-2��0����B��3��0����
��AB=3-��-2��=5��
�ߵ�C�������ǣ�-1��3����
��CG=3��CH=1��
��${S}_{��ABC}=\frac{1}{2}AB•AC=\frac{1}{2}��5��3=\frac{15}{2}$��
��${S}_{��COM}=\frac{15}{4}$��
��$\frac{1}{2}OM•CH=\frac{15}{4}$��
��OM=$\frac{15}{2}=7.5$��
���M�������ǣ�0��-7.5����
��3���ߵ�M�������ǣ�0��-7.5��ʱ����COM�����=$\frac{1}{2}$��ABC�������
���M�������ǣ�0��7.5��ʱ����COM�����=$\frac{1}{2}$��ABC�������
�������εĸ�һ��ʱ������͵׳����ȣ�
���M�������ǣ�2.5��0����-2.5��0��ʱ��
��COM�����=$\frac{1}{2}$��ABC�������
���ϣ��ɵ�
�������������λ�ô��ڵ�M��ʹ���ۡ���COM�����=$\frac{1}{2}$��ABC���������Ȼ������
���������ĵ�M��������3������0��7.5������2.5��0����-2.5��0����
���� ��1��������Ҫ������������ͼ�ε����ʺ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ���ٵ�x��ľ������������йأ���y��ľ�����������йأ��ھ��붼�ǷǸ���������������Ǹ��������ɾ���������ʱ����Ҫ����ǡ���ķ��ţ�
��2����������������ε��������Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2cm | B�� | 3cm | C�� | 4cm | D�� | 6cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�AC��BD�ཻ��O��E��CD���е㣬����OE����BCD���ܳ�Ϊ10�����ODE���ܳ�Ϊ5��
��ͼ����?ABCD�У�AC��BD�ཻ��O��E��CD���е㣬����OE����BCD���ܳ�Ϊ10�����ODE���ܳ�Ϊ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 7 | C�� | -4 | D�� | -8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 1 | C�� | 0 | D�� | $-\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
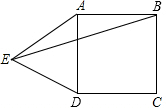 ��ͼ����������ABCD����࣬���ȱ�������ADE�����AEB=��������
��ͼ����������ABCD����࣬���ȱ�������ADE�����AEB=��������| A�� | 10�� | B�� | 15�� | C�� | 30�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com