
【题目】如图①,在△ABC中,AB=AC,BC=acm,∠B=30°.动点P以1cm/s的速度从点B出发,沿折线B﹣A﹣C运动到点C时停止运动.设点P出发x s时,△PBC的面积为y cm2 . 已知y与x的函数图象如图②所示.请根据图中信息,解答下列问题: 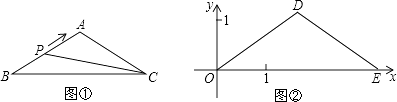
(1)试判断△DOE的形状,并说明理由;
(2)当a为何值时,△DOE与△ABC相似?
【答案】
(1)解:△DOE是等腰三角形.
理由如下:过点A作AM⊥BC于M,
∵AB=AC,BC=acm,∠B=30°,
∴AM= ![]() ×
× ![]() =
= ![]() a,AC=AB=
a,AC=AB= ![]() a,
a,
∴S△ABC= ![]() BCAM=
BCAM= ![]() a2,
a2,
∴P在边AB上时,
y= ![]() S△ABC=
S△ABC= ![]() ax,
ax,
P在边AC上时,
y= ![]() S△ABC=
S△ABC= ![]() a2﹣
a2﹣ ![]() ax,
ax,
作DF⊥OE于F,
∵AB=AC,点P以1cm/s的速度运动,
∴点P在边AB和AC上的运动时间相同,
∴点F是OE的中点,
∴DF是OE的垂直平分线,
∴DO=DE,
∴△DOE是等腰三角形
(2)解:由题意得:∵AB=AC,BC=acm,∠B=30°,
∴AM= ![]() ×
× ![]() =
= ![]() a,
a,
∴AB= ![]() a,
a,
∴D( ![]() a,
a, ![]() a2),
a2),
∵DO=DE,AB=AC,
∴当且仅当∠DOE=∠ABC时,△DOE∽△ABC,
在Rt△DOF中,tan∠DOF= ![]() =
= ![]() =
= ![]() a,
a,
由 ![]() a=tan30°=
a=tan30°= ![]() ,得a=
,得a= ![]() ,
,
∴当a= ![]() 时,△DOE∽△ABC.
时,△DOE∽△ABC.
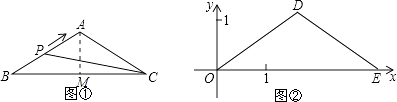
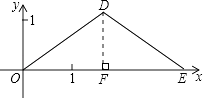
【解析】(1)首先作DF⊥OE于F,由AB=AC,点P以1cm/s的速度运动,可得点P在边AB和AC上的运动时间相同,即可得点F是OE的中点,即可证得DF是OE的垂直平分线,可得△DOE是等腰三角形;(2)设D( ![]() a,
a, ![]() a2),由DO=DE,AB=AC,可得当且仅当∠DOE=∠ABC时,△DOE∽△ABC,然后由三角函数的性质,即可求得当a=
a2),由DO=DE,AB=AC,可得当且仅当∠DOE=∠ABC时,△DOE∽△ABC,然后由三角函数的性质,即可求得当a= ![]() 时,△DOE∽△ABC.
时,△DOE∽△ABC.
【考点精析】关于本题考查的相似三角形的性质和解直角三角形,需要了解对应角相等,对应边成比例的两个三角形叫做相似三角形;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC. 
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至上海的铁路里程为650km.从徐州乘“C”字头列车A,“D”字头列车B都可到达上海,已知A车的平均速度为B车的2倍,且行驶时间比B车少2.5h.
(1)设A车的平均速度是xkm/h,根据题意,可列分式方程:;
(2)求A车的平均速度及行驶时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为16m的正方形展厅,准备用边长分别为1m和0.5m的两种正方形地板砖铺设其地面.要求正中心一块是边长为1m的大地板砖,然后从内到外一圈小地板砖、一圈大地板砖相间镶嵌(如图所示),则铺好整个展厅地面共需要边长为1m的大地板砖块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F. 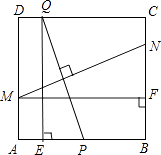
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F. 
(1)△ABC与△FOA相似吗?为什么?
(2)试判定四边形AFCE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com