
【题目】已知函数![]() .
.
(1)请在平面直角坐标系中画出该函数的图象,
(2)若点![]() 在该函数图象上,且当
在该函数图象上,且当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时都以同样价格出售相同的商品,“五一”期间两家商场都让利酬宾.其中甲商场所有商品直接打折销售,乙商场在购买一定数额商品后,超过部分打折售.设商品的原价为![]() 元,购买商品后实付金额为
元,购买商品后实付金额为![]() 元,
元,![]() 与
与![]() 之间的函数关系如图所示:
之间的函数关系如图所示:

(1)求![]() 的值;
的值;
(2)说出甲乙两家商场的具体销售方式;
(3)“五一”期间,选择哪家商场去购物更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
小明和小丽共同探究一道数学题:
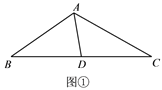
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
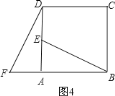
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,

AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
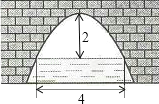
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
A.3 B.2![]() C.3
C.3![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中, ![]() ,D、E是斜边BC上两点,且∠DAE=45°,将△
,D、E是斜边BC上两点,且∠DAE=45°,将△![]() 绕点
绕点![]() 顺时针旋转90
顺时针旋转90![]() 后,得到△
后,得到△![]() ,连接
,连接![]() .列结论:
.列结论:
①△ADC≌△AFB;②△ ![]() ≌△
≌△![]() ;③△
;③△![]() ≌△
≌△![]() ;④
;④![]()
其中正确的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
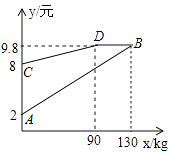
【题目】2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
(1)请你解释图中点B的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的y1与x之间的函数解析式;
(3)当0<x≤90时,求该葵花籽的产量为多少时,该企业获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
如图![]() ,以
,以![]() 为轴,把
为轴,把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
如图![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使![]() 变到
变到![]() 的位置;
的位置;
②指图中线段![]() 与
与![]() 之间的关系,为什么?
之间的关系,为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com