
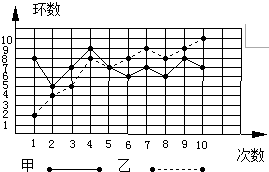
| A. | 甲、乙的总环数相等 | B. | 甲的成绩稳定 | ||
| C. | 甲、乙的众数相同 | D. | 乙的发展潜力更大 |
科目:初中数学 来源: 题型:解答题
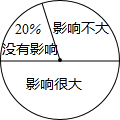 近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数(人) | 40 | 60 | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
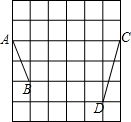 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
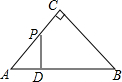 如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )| A. | 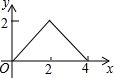 | B. | 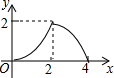 | C. | 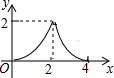 | D. | 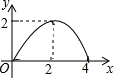 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
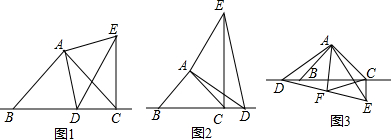
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
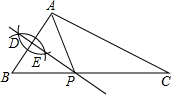 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )| A. | PA+PC=BC | B. | PA=PB | C. | DE⊥AB | D. | PA=PC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com