
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为______.
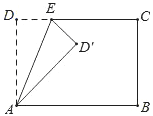
【答案】2或32.
【解析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
解:如图1,
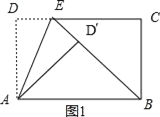
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B、D′、E三点共线,
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=17,
∵BD′=![]() =15,
=15,
∴DE=D′E=17﹣15=2;
如图2,
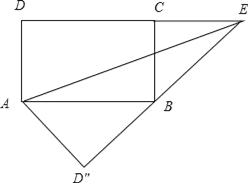
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∠D″=∠BCE,AD″=BC,∠CBE=∠BAD″,
∴△ABD″≌△BEC,
∴BE=AB=17,
∴DE=D″E=17+15=32.
综上所知,DE=2或32.
故答案为:2或32.
“点睛”翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.


科目:初中数学 来源: 题型:
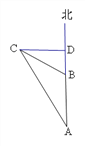
【题目】如图,一艘轮船从A处向正北方向航行,达到B处后,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,若DB等于36海里,求B到CA的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
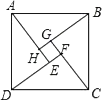
A. 8 B. 6 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
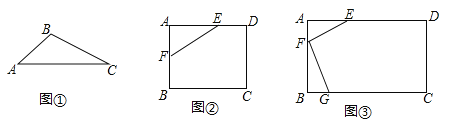
(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
问题探究
(2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
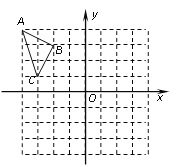
【题目】在如图的方格纸中,每个小正方形的边长都为l,△ABC的顶点坐标分别为A(-4,4)、B(-2,3)、C(-3,1).
(1)在图中画出与△ABC关于y轴对称的△A1B1C1,并直接写出△A1B1C1的三个顶点坐标;
(2)画出将△A1B1C1向下平移4格得到的△A2B2C2,并直接写出△A2B2C2的三个顶点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用自己节省的零花钱购买一台MP5来学习英语,他已存有50元,并计划从本月起每月节省30元,直到他至少有280元.设x个月后小刚至少有280元,则可列计算月数的不等式为( )
A.30x+50>280
B.30x-50≥280
C.30x-50≤280
D.30x+50≥280
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com