
【题目】如图①,在△ABC中,AE平分∠BAC,∠C>∠B,F是AE上一点,且FD⊥BC于D点.
(1)试猜想∠EFD,∠B,∠C的关系,并说明理由;
(2)如图②,当点F在AE的延长线上时,其余条件不变,(1)中的结论还成立吗?说明理由.

① ②
【答案】(1)∠EFD=![]() ∠C-
∠C-![]() ∠B.()成立,理由见解析.
∠B.()成立,理由见解析.
【解析】
先根据AE平分∠BAC推出∠BAE=![]() ∠BAC=
∠BAC=![]() [180°-(∠B+∠C)],再根据外角的定义求出∠FED=∠B+∠BAE,然后利用直角三角形的性质求出∠EFD=90°-∠FED.
[180°-(∠B+∠C)],再根据外角的定义求出∠FED=∠B+∠BAE,然后利用直角三角形的性质求出∠EFD=90°-∠FED.
解:(1)∠EFD=![]() ∠C-
∠C-![]() ∠B.
∠B.
理由如下:由AE是∠BAC的平分线知∠BAE=![]() ∠BAC.
∠BAC.
由三角形外角的性质知∠FED=∠B+![]() ∠BAC,
∠BAC,
故∠B+![]() ∠BAC+∠EFD=90°①.
∠BAC+∠EFD=90°①.
在△ABC中,由三角形内角和定理得
∠B+∠BAC+∠C=180°,
即![]() ∠C+
∠C+![]() ∠B+
∠B+![]() ∠BAC=90°②.
∠BAC=90°②.
②-①,得∠EFD=![]() ∠C-
∠C-![]() ∠B.
∠B.
(2)成立.
理由如下:由对顶角相等和三角形的外角性质知:∠FED=∠AEC=∠B+![]() ∠BAC,
∠BAC,
故∠B+![]() ∠BAC+∠EFD=90°①.
∠BAC+∠EFD=90°①.
在△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,即![]() ∠B+
∠B+![]() ∠BAC+
∠BAC+![]() ∠C=90°②.②-①,得∠EFD=
∠C=90°②.②-①,得∠EFD=![]() ∠C-
∠C-![]() ∠B.
∠B.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,由于经营不善,经常导致牛奶滞销(没卖完)或脱销(量不够),为此细心的小红结合所学知识帮奶奶统计了一个星期牛奶的销售情况,并绘制成下表:
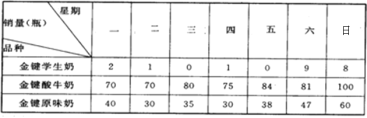
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高;
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定;
(3)假如你是小红,会给奶奶哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为s时,△ADP是等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x=____________°;x=____________°;x=____________°;
(3)如图③,一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F=________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题。 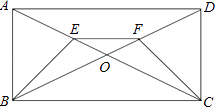
(1)用适当的方法解下列一元二次方程:x2﹣6x+1=0.
(2)如图,已知E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF,求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
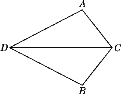
【题目】如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com