
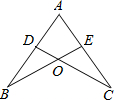
 如图,已知点D在AB上,点E在AC上,AB=AC,请你再补充一个条件,使△ABE≌△ACD.你补充的条件是∠B=∠C或AD=AE.
如图,已知点D在AB上,点E在AC上,AB=AC,请你再补充一个条件,使△ABE≌△ACD.你补充的条件是∠B=∠C或AD=AE. 分析 在△ABE与△ACD中,已知一组对应边相等、一组对应角相等,所以添加另外一组对应边(角)相等即可推知△ABE≌△ACD.
解答 解:∠B=∠C,
理由是:∵在△ABE和△ACD中,
$\left\{\begin{array}{l}{∠A=∠A}\\{AB=AC}\\{∠B=∠C}\end{array}\right.$,
∴△ABE≌△ACD(ASA).
或者添加AD=AE.
理由是:∵在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD(SAS).
或者添加AD=AE.
故答案是:∠B=∠C或AD=AE.
点评 本题考查了全等三角形的判定定理的应用,能理解全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
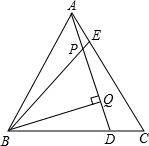 如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.
如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com