
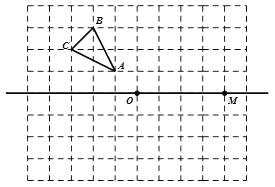
【题目】如图,它是一个8×10的网格,每个小正方形的边长均为1 ,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△![]() .
.
(2)画出△ABC关于点O的中心对称图形△![]() .
.
(3)△![]() 与△
与△![]() 组成的图形是轴对称图形吗?如果是,请画出对称轴.△
组成的图形是轴对称图形吗?如果是,请画出对称轴.△![]() 与△
与△![]() 组成的图形__________(填“是”或“不是”)轴对称图形.
组成的图形__________(填“是”或“不是”)轴对称图形.
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①所有的有理数都能用数轴上的点表示;
②符号不同的两个数互为相反数;
③有理数分为正数和负数;
④两数相减,差一定小于被减数;
⑤两数相加,和一定大于任何一个加数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一块长与宽之比为2∶1的铁皮的四角各剪去一个边长为10 cm的小正方形,折起四边,可以做成一个无盖的盒子.如果这个盒子的容积是1 500 cm3,那么铁皮的长和宽各是多少?若设铁皮的宽为x cm,则正确的方程是( )
A. (2x-20)(x-20)=1 500 B. (2x-10)(x-20)=1 500
C. 10(2x-20)(x-20)=1 500 D. 10(x-10)(x-20)=1 500
查看答案和解析>>
科目:初中数学 来源: 题型:
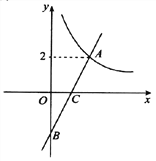
【题目】如图在平面直角坐标系xOy中,函数![]() (
(![]() )的图象与一次函数
)的图象与一次函数![]() 的图象的交点为A(m,2).
的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)观察图像直接写出使得![]() 的
的![]() 的取值范围;
的取值范围;
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规定学生的数学学期评定成绩满分为100,其中平时成绩占50%,期中考试成绩占20%,期末考试成绩占30%.小红的三项成绩(百分制)依次是86、70、90,小红这学期的数学学期评定成绩是( )
A. 90B. 86C. 84D. 82
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
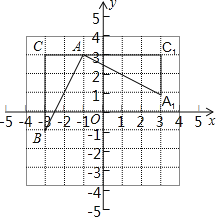
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
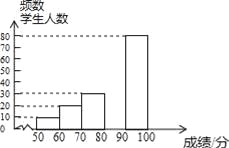
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com