
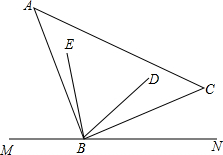
 如图,点B在直线MN上,三角板的直角顶点与点B重合,∠NBD:∠DBE:∠EBM=2:3:4,
如图,点B在直线MN上,三角板的直角顶点与点B重合,∠NBD:∠DBE:∠EBM=2:3:4,分析 (1)根据已知条件和平角的定义列方程即可得到结论;
(2)根据平角的定义得到∠MBA+∠NBC=90°,由射线BA平分∠DBM,推出BC平分∠NBD,求得∠CBD=$\frac{1}{2}∠$NBD=20°,即可得到结论.
解答 解:(1)∵∠NBD:∠DBE:∠EBM=2:3:4,
∠NBD+∠DBE+∠EBM=180°,
∴∠NBD=40°;
(2)∵∠ABC=90°,
∴∠MBA+∠NBC=90°,
当射线BA平分∠DBM时,
BC平分∠NBD,
∴∠CBD=$\frac{1}{2}∠$NBD=20°,
∵∠DBE=$\frac{3}{2+3+4}$×180°=60°,
∴∠EBC=80°,
∴当∠EBC=80°时,射线BA平分∠DBM.
故答案为:80.
点评 本题考查了角的计算,角平分线的定义,平角的定义,熟记角平分线的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 当x≤1时,y随x的增大而减小 | B. | 当x≥1时,y随x的增大而增大 | ||
| C. | 当x<3时,y随x的增大而减小 | D. | 当x>3时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
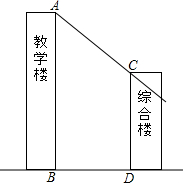 如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)
如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
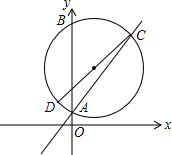 如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.
如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
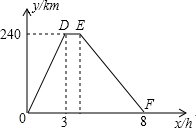 小王从A地前往B地送货,到达B地后,休息1h后按原路返回,他与A地的距离y(单位:km)和所用的时间x(单位;h)之间的函数关系式如图所示.
小王从A地前往B地送货,到达B地后,休息1h后按原路返回,他与A地的距离y(单位:km)和所用的时间x(单位;h)之间的函数关系式如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
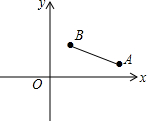 如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.
如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com