
【题目】如图,已知直线l1∥l2 , l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;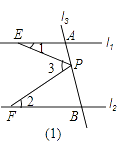
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;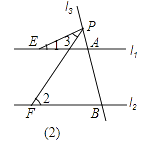
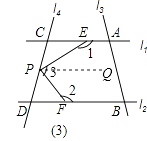
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.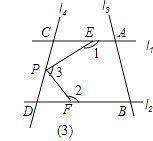
【答案】
(1)证明:过P作PQ∥l1∥l2,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
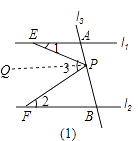
(2)解:关系:∠3=∠2﹣∠1;
过P作直线PQ∥l1∥l2,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
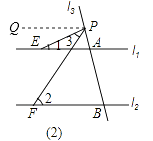
(3)解:关系:∠3=360°﹣∠1﹣∠2.
过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
【解析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲,乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)将下表填完整:
身高 | 176 | 177 | 178 | 179 | 180 |
甲队(人数) | 3 | 4 | |||
乙队(人数) | 2 | 1 | 1 |
(2)甲队队员身高的平均数为cm,乙队队员身高的平均数为cm;
(3)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
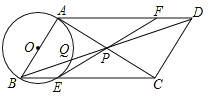
【题目】如图,在ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.
(1)求证:EF是⊙O的切线;
(2)求证:![]() =4BPQP.
=4BPQP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某织布厂有 150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣 4 件,制衣一件需要布 1.5m,将布直接出售,每米布可获利 2 元,将布制成衣后出售,每件可获利 25 元,若每名工人只能做一项工作,且不计其他因素,设安排 x 名工人制衣.
(1)一天中制衣所获利润 元(用含 x 的式表示);
(2)一天中销售剩余的布所获利润为 元(用含 x 的式表示);
(3)一天当中安排 名工人制衣时,所获利润为 13712 元;
(4)一年按 300 天计算,一年中这个工厂所获利润最大值为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
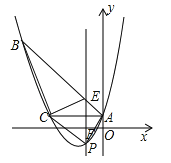
【题目】如图,已知抛物线![]() 经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 . 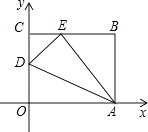
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com