
【题目】如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )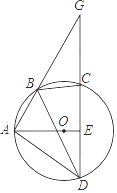
A.50°
B.60°
C.80°
D.90°
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,坐标原点O是菱形ABCD的对称中心.边AB与x轴平行,点B(1,-2),反比例函数 ![]() (k≠0)的图象经过A,C两点.
(k≠0)的图象经过A,C两点.
(1)求点C的坐标及反比例函数的解析式.
(2)直线BC与反比例函数图象的另一交点为E,求以O,C,E为顶点的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务. 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p= ![]() ,则三角形的面积S=
,则三角形的面积S= ![]() .
.
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c,则三角形的面积S= ![]() .
.
(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于 .
(2)若一个三角形的三边长分别是 ![]() ,求这个三角形的面积.
,求这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识链接】 有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: ![]() 的有理化因式是
的有理化因式是 ![]() ;1﹣
;1﹣ ![]() 的有理化因式是1+
的有理化因式是1+ ![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:![]() =
= ![]() =
= ![]() ﹣1,
﹣1, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)【知识理解】 填空:2 ![]() 的有理化因式是;
的有理化因式是;
直接写出下列各式分母有理化的结果:
① ![]() =;②
=;② ![]() = .
= .
(2)【启发运用】 计算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则![]() ,
, ![]() .在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A. (0,0) B. (0,2)
C. (2,-4) D. (-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com