
分析 过O点作OD⊥AB,则AD=6cm,因为∠OAD=30°,根据直角三角形中的三角函数可得tan30°=$\frac{DO}{AD}$求出DO,进而可得出结论.
解答  解:如图,作OD⊥AB,
解:如图,作OD⊥AB,
∵等边三角形的边长为12厘米,
∴AD=6厘米.
又∵∠DAO=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
∴tan30°=$\frac{DO}{AD}$=$\frac{DO}{6}$=$\frac{\sqrt{3}}{3}$,
∴DO=2$\sqrt{3}$厘米,
∴其内切圆的面积=π(2$\sqrt{3}$)2=12π.
故答案为:12π平方厘米.
点评 本题考查了三角形的内切圆与内心,解这类题一般都利用过内心向正三角形的一边作垂线,则正三角形的半径、内切圆半径和正三角形边长的一半构成一个直角三角形,解这个直角三角形,可求出相关边长或角


科目:初中数学 来源: 题型:选择题
| A. | 3m2n与3nm2 | B. | $\frac{1}{3}$xy2与$\frac{1}{3}$x2y2 | C. | -5ab与-5×103ab | D. | 35与-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
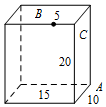 长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )
长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )| A. | $10\sqrt{5}+5$ | B. | $5\sqrt{29}$ | C. | 25 | D. | $5\sqrt{37}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
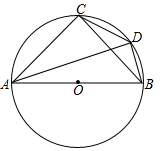 如图,△ABC是⊙O的内接等腰直角三角形,∠ACB=90°,点D为⊙O上的一点,满足BD=3,CD=4$\sqrt{2}$,连接AD,则AD的长为11.
如图,△ABC是⊙O的内接等腰直角三角形,∠ACB=90°,点D为⊙O上的一点,满足BD=3,CD=4$\sqrt{2}$,连接AD,则AD的长为11.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com