
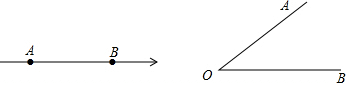
分析 (1)根据题意即可得到结果;
(2)①若点P在A的左侧,设点P表示的实数为x,②若点P在A的右侧,设点P表示的实数为x,列方程即可得到结论;
(3)如图,由点M、N分别是线段AP和线段BP的中点,得到PM=$\frac{1}{2}$AP=$\frac{1}{2}$(AB+PB),PN=$\frac{1}{2}$BP,根据线段的和差即可得到结论.
(4)由OM,ON分别平分∠AOP,∠BOP,得到∠POM=$\frac{1}{2}$∠AOP,∠PON=$\frac{1}{2}$∠BOP,根据角的和差即可得到结论.
解答 解:(1)线段AB的长度为b-a,
故答案为:b-a;
(2)①若点P在A的左侧,设点P表示的实数为x,
则a-x-(b-a)=1,
∴x=2a-b-1;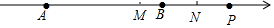
②若点P在A的右侧,设点P表示的实数为x,
则x-a-(b-a)=1,
∴x=b+1;
综上所述:点P表示的数为2a-b-1或b+1;
(3)如图,∵点M、N分别是线段AP和线段BP的中点,
∴PM=$\frac{1}{2}$AP=$\frac{1}{2}$(AB+PB),PN=$\frac{1}{2}$BP,
∴MN=PM-PN=$\frac{1}{2}$AB=$\frac{b-a}{2}$;
(4)题目:如图,∠AOB=m°,射线OP在∠AOB的外部,射线OM,ON分别平分∠AOP,∠BOP,求∠MON.
解:∵OM,ON分别平分∠AOP,∠BOP,
∴∠POM=$\frac{1}{2}$∠AOP,∠PON=$\frac{1}{2}$∠BOP,
∴∠POM-∠PON=$\frac{1}{2}∠$AOP-$\frac{1}{2}∠$BOP=$\frac{1}{2}$(∠AOP-∠BOP)=$\frac{1}{2}∠$AOB,
∵∠AOB=m°,
∴∠MON=∠POM-∠PON=$\frac{1}{2}$m°.
点评 本题考查了数轴和一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
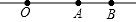 如图,下列不正确的说法是( )
如图,下列不正确的说法是( )| A. | 直线AB与直线BA是同一条直线 | B. | 射线OA与射线AB是同一条射线 | ||
| C. | 线段AB与线段BA是同一条线段 | D. | 射线OA与射线OB是同一条射线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
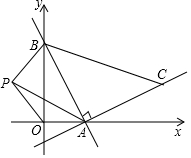 如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.
如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com